


: この文書について...
代数学II要約 No.7
今日のテーマ:
 これからは、特に断らない限りは「群
これからは、特に断らない限りは「群 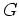 の表現」といえば
複素数体
の表現」といえば
複素数体
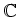 上のものを考えることにする。
上のものを考えることにする。
No.6 でも少し述べたように、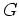 -加群の間の
-加群の間の 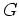 -準同型は次のように定義される。
-準同型は次のように定義される。
定義 7.1
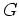
-加群
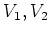
の間の線型写像
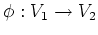
が
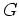
-準同型であるとは、
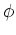
が
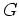
の作用を保つ、すなわち
任意の
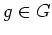
と任意の
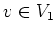
とに対して、
が成り立つときに言う。
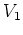
から
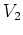
への
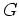
-線型写像の全体はそれ自身線型空間になる。
これを
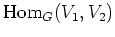
とかく。
一般に、線型写像の「平均」をとることによって 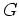 -準同型を
得ることができるわけだが、そもそも
-準同型を
得ることができるわけだが、そもそも 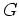 -準同型自体は
そんなに多くはない。
-準同型自体は
そんなに多くはない。
定義 7.2
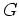
-加群
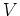
が、非自明な
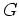
-部分加群(0,
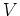
以外の
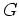
-部分加群)をもたない
とき、
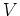
は既約な
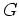
-加群であるとよばれる。
マシュケの定理を用いると、次のことが分かる。
補題 7.1 (マシュケの定理の系)
有限群
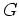
の(複素数体
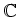
上の有限次元)表現
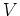
は、
必ず既約な
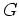
-加群の直和に分解する。
2003/6/8
![]() これからは、特に断らない限りは「群
これからは、特に断らない限りは「群 ![]() の表現」といえば
複素数体
の表現」といえば
複素数体
![]() 上のものを考えることにする。
上のものを考えることにする。
![]() -加群の間の
-加群の間の ![]() -準同型は次のように定義される。
-準同型は次のように定義される。
![]() -準同型を
得ることができるわけだが、そもそも
-準同型を
得ることができるわけだが、そもそも ![]() -準同型自体は
そんなに多くはない。
-準同型自体は
そんなに多くはない。