


: この文書について...
代数学II要約 No.8
今日のテーマ:

今回も表現は
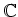 上のものを考えることにする。
上のものを考えることにする。
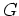 の表現は自然に群環
の表現は自然に群環
![$ {\mathbb{C}}[G]$](img4.png) -加群と見ることもできた。
-加群と見ることもできた。
![$ {\mathbb{C}}[G]$](img4.png) の構造を知ると
の構造を知ると 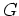 -加群の既約分解はかなり見通しがよくなる。
-加群の既約分解はかなり見通しがよくなる。
定義 8.1
環
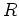
の元
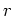
が中心元であるとは、
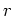
が
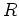
のどの元とも可換であるとき、
すなわち、
が成り立つときにいう。
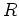
の中心元全体の集合を
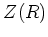
と書き、
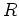
の
中心と呼ぶ。
補題 8.1
任意の環
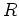
に対して、その中心
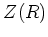
は可換環をなす。
群環
![$ {\mathbb{C}}[G]$](img4.png) の中心を求めるために、群論の次の事実を思い起こそう。
の中心を求めるために、群論の次の事実を思い起こそう。
定義 8.2 (復習)
一般に、群
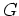
の元
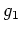
と
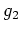
とが(
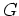
のなかで)共役であるとは、
ある
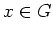
があって、
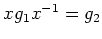
が成り立つときにいう。
共役という関係は
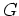
の一つの同値関係を与えていて、
その同値関係についてのそれぞれのクラスを共役類と呼ぶ。
各
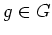
に対して、
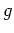
と共役なものの全体の集合をここでは
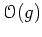
と書く。
さらに、共役なものについての和
のことを、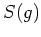 と書くことにする。(本講義の参考書(「加群十話」)では [g]
と書いてあるが、記号
と書くことにする。(本講義の参考書(「加群十話」)では [g]
と書いてあるが、記号![$ [\bullet]$](img18.png) は既に別の意味で用いたため、
ここだけ記号を変えてある。)
は既に別の意味で用いたため、
ここだけ記号を変えてある。)
これまで、群 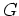 の元全体での平均をよく用いてきたが、
の元全体での平均をよく用いてきたが、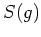 は「部分的な
平均」である。
は「部分的な
平均」である。
補題 8.2
![$ {\mathbb{C}}[G]$](img4.png)
の中心
![$ Z({\mathbb{C}}[G])$](img19.png)
は
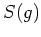
の一次結合の全体と一致する。
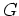 -加群(=
-加群(=
![$ {\mathbb{C}}[G]$](img4.png) )加群の分解は、まず
)加群の分解は、まず
![$ Z({\mathbb{C}}[G])$](img19.png) の固有分解から
行うのが楽になる。これについては次回。
の固有分解から
行うのが楽になる。これについては次回。
問題 8.1
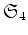
の共役類によるクラス分けを書き、
それぞれの類
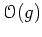
について
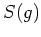
を
もとめなさい。
問題 8.2
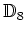
の共役類によるクラス分けを書き、
それぞれの類
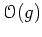
について
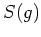
を
もとめなさい。
2003/6/11
![]()
![]() 上のものを考えることにする。
上のものを考えることにする。
![]() の表現は自然に群環
の表現は自然に群環
![]() -加群と見ることもできた。
-加群と見ることもできた。
![]() の構造を知ると
の構造を知ると ![]() -加群の既約分解はかなり見通しがよくなる。
-加群の既約分解はかなり見通しがよくなる。
![]() の中心を求めるために、群論の次の事実を思い起こそう。
の中心を求めるために、群論の次の事実を思い起こそう。
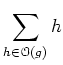
![]() の元全体での平均をよく用いてきたが、
の元全体での平均をよく用いてきたが、![]() は「部分的な
平均」である。
は「部分的な
平均」である。
![]() -加群(=
-加群(=
![]() )加群の分解は、まず
)加群の分解は、まず
![]() の固有分解から
行うのが楽になる。これについては次回。
の固有分解から
行うのが楽になる。これについては次回。