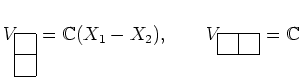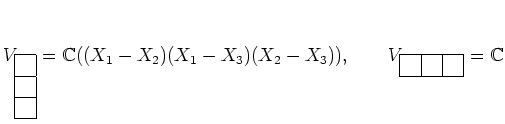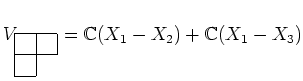 等々
等々
今回は、気分を変えて、対称群の既約表現を実際に与える方法について(証明は抜きで)述べよう。
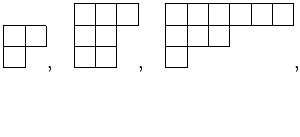
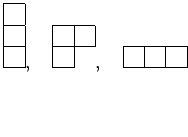
ヤング図形とは、正方形の箱を、縦横に次のような恰好で 並べたものである。
 等々
等々
正方形の数が![]() 個のヤング図形のことを、
個のヤング図形のことを、![]() 次のヤング図形という。
実は
次のヤング図形という。
実は ![]() 次の対称群
次の対称群
![]() の既約表現は、
の既約表現は、
![]() -次のヤング図形の分だけあって、
実際にそこから構成できることが知られている。
つまり、
-次のヤング図形の分だけあって、
実際にそこから構成できることが知られている。
つまり、
![]() の既約表現は
の既約表現は
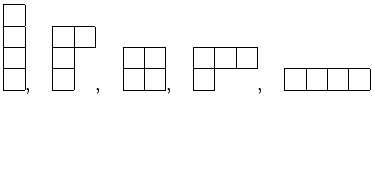
![]() 次のヤング図形
次のヤング図形 ![]() をひとつとって
そのおのおのの正方形に
をひとつとって
そのおのおのの正方形に ![]() から
から ![]() までの数字を
だぶらないように書き入れたものを(
までの数字を
だぶらないように書き入れたものを(![]() を台とする)ヤングの盤という。
ヤングの盤には、次のような調子で多項式を対応させることができる。
を台とする)ヤングの盤という。
ヤングの盤には、次のような調子で多項式を対応させることができる。
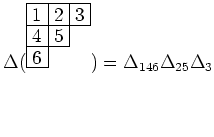
![]() の元は
の元は ![]() -変数の多項式の全体に文字の置き換えで作用する。
-変数の多項式の全体に文字の置き換えで作用する。
![]() の形の多項式に
の形の多項式に
![]() の元を作用すると、
の元を作用すると、 ![]() と同じ台を
もって文字をつけ替えたような別のヤングの盤
と同じ台を
もって文字をつけ替えたような別のヤングの盤 ![]() があって、
があって、
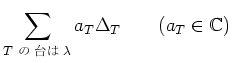
実は、![]() どうしは独立ではなく、関係式が幾つかあることに
注意せねばならない。
どうしは独立ではなく、関係式が幾つかあることに
注意せねばならない。
![]() の既約表現は次の空間で与えられる。
の既約表現は次の空間で与えられる。