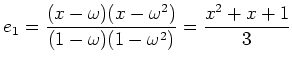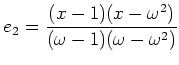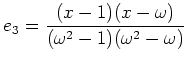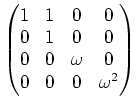: この文書について...
代数学II 試験略解
問題 14.1
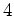
次のヤング図形
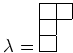
について、
![$ {\mathbb{C}}[\mathfrak{S}_4]$](img3.png)
の元
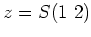
が表現
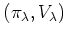
上
どのような作用を行うか記述しなさい。
(略解)
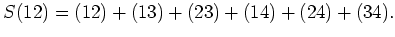 |
(★) |
これを
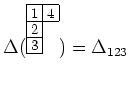 に作用させることを
考えればよい。
(★)の右辺の最初の3項は
に作用させることを
考えればよい。
(★)の右辺の最初の3項は
 に
に 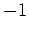 倍で作用する。
あとの3項が問題だが、
倍で作用する。
あとの3項が問題だが、
とやって、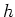 を計算すればよいわけだ。素直に計算してもよいが、次のように
考えると楽になる。
命題9.1により、
を計算すればよいわけだ。素直に計算してもよいが、次のように
考えると楽になる。
命題9.1により、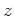 の作用は定数倍であるはずであることが分かっているので、
の作用は定数倍であるはずであることが分かっているので、
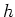 は当然
は当然
 の倍数でなければならないわけである。
すなわち、展開すると
の倍数でなければならないわけである。
すなわち、展開すると 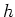 は
は 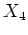 を含まない式になる。したがって、
となっているはずであり、右辺はすぐに
を含まない式になる。したがって、
となっているはずであり、右辺はすぐに
 と等しいことが
確かめられる。
と等しいことが
確かめられる。
まとめると、
すなわち 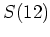 は
は 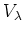 上
上 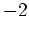 倍として作用する。
(命題9.1 により、
倍として作用する。
(命題9.1 により、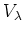 上
上 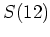 はスカラーとして作用するから、
上のように
はスカラーとして作用するから、
上のように
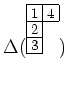 への作用を考えるだけで
十分であるのだが、納得がいかない人は
への作用を考えるだけで
十分であるのだが、納得がいかない人は
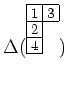 等の上の作用を検討してみてもよい。
文字の付け替えだけで同じことをしているのが理解できると思う。)
等の上の作用を検討してみてもよい。
文字の付け替えだけで同じことをしているのが理解できると思う。)
問題 14.2
![$ {\mathbb{C}}[\mathfrak{S}_4]$](img3.png)
の元
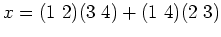
と、
4次のヤング図形
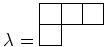
に対して、
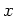
を
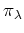
上で表現した行列
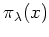
の
最小多項式を求めなさい。
(略解)
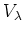 は次のように与えられる。
は次のように与えられる。
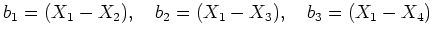 とおくと、
とおくと、
すなわち、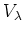 の基底として
の基底として
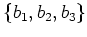 を採用したときの
を採用したときの
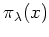 の表現行列は、
で与えられる。
この行列の特性多項式は
の表現行列は、
で与えられる。
この行列の特性多項式は
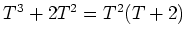 . 計算してみると分かるが、
最小多項式は
. 計算してみると分かるが、
最小多項式は 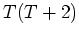 である。
(本問の
である。
(本問の 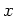 は
は
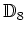 の群環の中心元ともみることができ、
そうみなせば補題10.1を用いることもできる。)
の群環の中心元ともみることができ、
そうみなせば補題10.1を用いることもできる。)
問題 14.3
複素数体
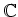
を部分環として含む環
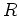
の元
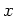
の最小多項式が
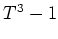
であるとき、次のような条件を同時に満足する
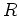
の元
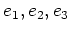
を
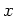
を用いて作りなさい。
-
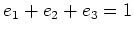
-
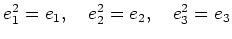
-
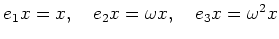
ただし、
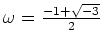
(
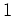
の3乗根の一つ)とする。
(略解)
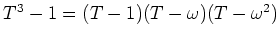 であり、
であり、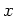 をその固有値によって
分解しようという問題である。
をその固有値によって
分解しようという問題である。
とやればよい。
問題 14.4
次のような条件を同時に満足する正方行列
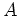
の例を挙げよ。(サイズは問わない)
ただし、
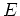
は(
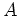
と同じサイズの)単位行列である。
-
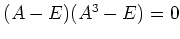
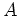 は非自明な3次の関係式を満足しない。
は非自明な3次の関係式を満足しない。
(略解)
例えば次のようなものがある。
ここに 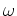 は 前問と同じ。
は 前問と同じ。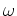 のような複素数を避けたい場合には、
のような複素数を避けたい場合には、
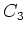 の表現を思い出しつつ、次のようなものを作ればよい。
の表現を思い出しつつ、次のようなものを作ればよい。
問題 14.5
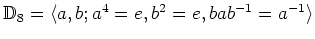
の
群環
![$ {\mathbb{C}}[\mathbb{D}_{8}]$](img67.png)
の元
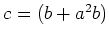
の(
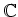
上の)
最小多項式を求めなさい。
(略解)
ゆえに、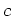 は
は 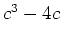 を満たす。
を満たす。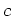 の最小多項式は
の最小多項式は
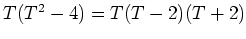 の約数ということになる。
の約数ということになる。  が2次の関係式を満たすのは不可能であるのが、
すぐに確かめられるから、
が2次の関係式を満たすのは不可能であるのが、
すぐに確かめられるから、
 の最小多項式は、ちょうど
の最小多項式は、ちょうど
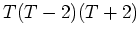 である。
である。



: この文書について...
平成15年7月30日
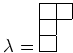 について、
について、
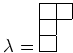 について、
について、
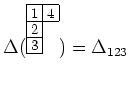 に作用させることを
考えればよい。
(★)の右辺の最初の3項は
に作用させることを
考えればよい。
(★)の右辺の最初の3項は
![]() に
に ![]() 倍で作用する。
あとの3項が問題だが、
倍で作用する。
あとの3項が問題だが、
![]() は
は ![]() 上
上 ![]() 倍として作用する。
(命題9.1 により、
倍として作用する。
(命題9.1 により、![]() 上
上 ![]() はスカラーとして作用するから、
上のように
はスカラーとして作用するから、
上のように
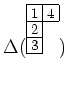 への作用を考えるだけで
十分であるのだが、納得がいかない人は
への作用を考えるだけで
十分であるのだが、納得がいかない人は
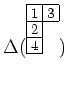 等の上の作用を検討してみてもよい。
文字の付け替えだけで同じことをしているのが理解できると思う。)
等の上の作用を検討してみてもよい。
文字の付け替えだけで同じことをしているのが理解できると思う。)
![]() は次のように与えられる。
は次のように与えられる。
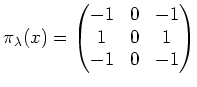
![]() であり、
であり、![]() をその固有値によって
分解しようという問題である。
をその固有値によって
分解しようという問題である。