


: この文書について...
代数学I特論要約 No.1
今日のテーマ
体の定義を思い起こそう。基本は、「加減乗除がそのなかでできるような集合」
ということであるが、ここではもう少し精密なところまで思い出しておく。
定義 1.1
集合
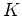
が体であるとは、
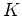
に「加法」と呼ばれる演算
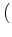
+
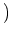
と、
「乗法」と呼ばれる演算
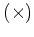
が定義されていて、
次の性質を満たすときにいう。
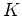 は加法について可換群をなす。(加法に関する単位元を普通 0
と表記する。)
は加法について可換群をなす。(加法に関する単位元を普通 0
と表記する。)
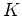 は乗法について可換半群をなす(つまり、乗法について
結合法則と交換法則が成り立つ)。
は乗法について可換半群をなす(つまり、乗法について
結合法則と交換法則が成り立つ)。
- 分配法則が成り立つ。
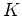 は(乗法に関する) 単位元をもつ。
は(乗法に関する) 単位元をもつ。
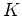 の 0 以外の各元は
の 0 以外の各元は 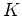 のなかに(乗法に関する) 逆元をもつ。
のなかに(乗法に関する) 逆元をもつ。
補題 1.1
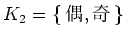
とおき、
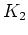
に次のような和と積を導入しよう。
この時 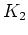 はこの演算で体であることがわかる。
はこの演算で体であることがわかる。
上の補題で、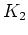 の元を 偶、奇 と書いたのは便宜上で、別に
の元を 偶、奇 と書いたのは便宜上で、別に 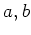 でも、
ア、イでも、その他何でも構わない。
でも、
ア、イでも、その他何でも構わない。
我々の体 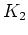 においては、
においては、
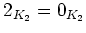 、もっと簡単に書くと
、もっと簡単に書くと
が成り立っている。(それ以外は普通の加法、乗法である。)
もっと一般に、ひとつひとつの素数 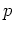 にたいして
が成り立つような体
にたいして
が成り立つような体 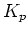 がそれぞれ存在する。
このような体についても代数の一般論が展開され、
重要な結果がいろいろと知られている。
(それらは、CD, DVD, 本の ISBN コード、コンピュータの通信手段、デジタル放送
など様々な場所で用いられている。)
がそれぞれ存在する。
このような体についても代数の一般論が展開され、
重要な結果がいろいろと知られている。
(それらは、CD, DVD, 本の ISBN コード、コンピュータの通信手段、デジタル放送
など様々な場所で用いられている。)
本講義では
これらの体をどう扱うか、そしてどのような結果が知られているかについて
講述したい。
問題 1.1
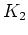
に対して、分配法則
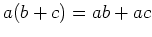
が成立することを総当たりで示しなさい。
平成17年1月4日
![]()
![]() はこの演算で体であることがわかる。
はこの演算で体であることがわかる。![]() の元を 偶、奇 と書いたのは便宜上で、別に
の元を 偶、奇 と書いたのは便宜上で、別に ![]() でも、
ア、イでも、その他何でも構わない。
でも、
ア、イでも、その他何でも構わない。
![]() においては、
においては、
![]() 、もっと簡単に書くと
、もっと簡単に書くと