


: この文書について...
代数学I特論要約 No.3
今日のテーマ

体 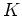 上の線型代数、
とくに、行列、その和、差、積、行列式、線型方程式の解法(掃き出し法、
クラメールの公式)などは
上の線型代数、
とくに、行列、その和、差、積、行列式、線型方程式の解法(掃き出し法、
クラメールの公式)などは
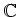 や
や
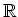 上の場合と全く同様に扱える。
上の場合と全く同様に扱える。
例えば
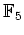 上の行列
上の行列
の逆行列を求めてみよう。通常と同様に、それは
で与えられる。注意せねばならないことは、
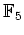 での
での 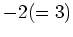 の逆元は
の逆元は 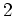 であるということである。すなわち
である。
であるということである。すなわち
である。
体 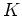 上の多項式を考えることもできる。
上の多項式を考えることもできる。
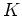 上の(
上の(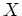 を変数とする)一変数多項式の全体は環をなし、それを
を変数とする)一変数多項式の全体は環をなし、それを ![$ K[X]$](img12.png) と書く。
多項式の既約性なども
と書く。
多項式の既約性なども
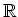 上のものと同様に定義される。
上のものと同様に定義される。
補題 3.1
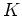
上の 一変数多項式
![$ f\in K[X]$](img13.png)
が二次式もしくは三次式であるとき、
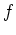
が (
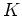
上の多項式として)既約であるための必要十分条件は、
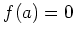
となる元
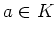
が存在することである。
問題 3.1
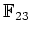
上の行列
の行列式と逆行列を求めなさい。
問題 3.2
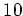
以上の素数
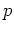
を適当に選んで、
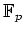
上既約な3次式の例を一つ挙げなさい。
理由も忘れずに書くこと。
平成16年10月18日
![]()
![]() 上の線型代数、
とくに、行列、その和、差、積、行列式、線型方程式の解法(掃き出し法、
クラメールの公式)などは
上の線型代数、
とくに、行列、その和、差、積、行列式、線型方程式の解法(掃き出し法、
クラメールの公式)などは
![]() や
や
![]() 上の場合と全く同様に扱える。
上の場合と全く同様に扱える。
![]() 上の行列
上の行列
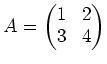
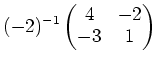
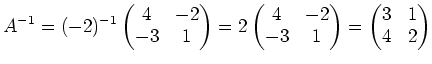
![]() 上の多項式を考えることもできる。
上の多項式を考えることもできる。
![]() 上の(
上の(![]() を変数とする)一変数多項式の全体は環をなし、それを
を変数とする)一変数多項式の全体は環をなし、それを ![]() と書く。
多項式の既約性なども
と書く。
多項式の既約性なども
![]() 上のものと同様に定義される。
上のものと同様に定義される。
