: この文書について...
代数学I特論要約 No.5
今日のテーマ

体 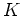 に対して、
に対して、
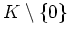 は(乗法に関して)群をなす。
これを
は(乗法に関して)群をなす。
これを 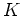 の乗法群と呼び、
の乗法群と呼び、 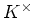 で書き表す。
で書き表す。
参考: 一般に、(単位元をもつ結合的な)環 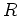 に対して
に対して
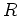 の元で、
の元で、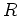 内に逆元をもつようなものの全体を
内に逆元をもつようなものの全体を 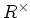 と書く。
と書く。
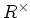 も乗法に関して群をなす。)
も乗法に関して群をなす。)
有限群 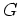 に対して、
に対して、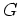 の元の個数(位数)を
の元の個数(位数)を 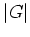 と書くと
と書くと
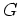 の任意の元
の任意の元 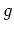 は
は
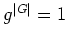 を満たすこと(ラグランジュの定理)
を思い出しておこう。
を満たすこと(ラグランジュの定理)
を思い出しておこう。
補題 5.1
有限体
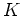
に対して、
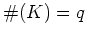
と書くと、
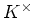
の任意の元
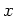
に対して、
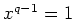
がなりたつ。
系 5.1
有限体
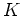
に対して、
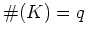
と書くと、
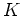
の任意の元
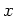
に対して、
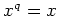
がなりたつ。とくに、
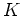
の元は
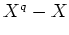
の根の全体と
ちょうど一致する。
系 5.2
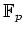
上の既約
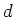
-次式は必ず
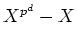
の約数である。
問題 5.1
-
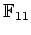 の(次数が2以上の)既約多項式
の(次数が2以上の)既約多項式 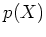 を一つ
選びなさい。
を一つ
選びなさい。
- 上の
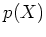 に対して、
に対して、
![$ K={\mathbb{F}}_{11}[X]/p(X){\mathbb{F}}_{11}[X]$](img23.png) のなかの
のなかの 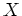 のクラスを
のクラスを
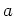 とおく。この時、
とおく。この時、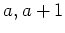 の逆元をそれぞれ求めなさい。
の逆元をそれぞれ求めなさい。
問題 5.2
二桁以上の素数
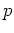
を二つ選んで、それぞれに対して
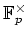
の
生成元を一つ挙げなさい。
問題 5.3
「参考」の部分、
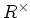
が群であることの証明をせよ。
平成16年11月2日
![]()
![]() に対して、
に対して、
![]() は(乗法に関して)群をなす。
これを
は(乗法に関して)群をなす。
これを ![]() の乗法群と呼び、
の乗法群と呼び、 ![]() で書き表す。
で書き表す。
![]() に対して
に対して
![]() の元で、
の元で、![]() 内に逆元をもつようなものの全体を
内に逆元をもつようなものの全体を ![]() と書く。
と書く。
![]() も乗法に関して群をなす。)
も乗法に関して群をなす。)
![]() に対して、
に対して、![]() の元の個数(位数)を
の元の個数(位数)を ![]() と書くと
と書くと
![]() の任意の元
の任意の元 ![]() は
は
![]() を満たすこと(ラグランジュの定理)
を思い出しておこう。
を満たすこと(ラグランジュの定理)
を思い出しておこう。