: この文書について...
代数学I特論要約 No.06
今日のテーマ
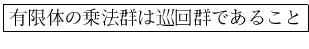
定義 06.1 (オイラーの関数)
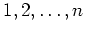
の中で、
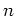
と互いに素な数の個数を
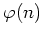
と書く。
補題 06.1
位数
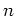
の巡回群を
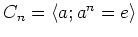
とかく。このとき、
-
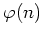 は、
は、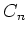 の
生成元(=位数がちょうど
の
生成元(=位数がちょうど 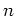 と一致するもの)の個数と等しい。
と一致するもの)の個数と等しい。
- 一般に、
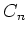 の元のうち位数がちょうど
の元のうち位数がちょうど 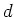 に一致するものの
個数は、
であたえられる。
に一致するものの
個数は、
であたえられる。
補題 06.2
体
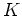
の乗法群
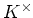
の元で、位数が
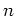
のものは
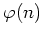
個
以下である。
命題 06.1
有限体
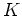
の乗法群
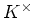
は必ず巡回群である。
有限体の元の個数は必ず素数の巾だったことを思い出しておこう。逆に、
次のことが成り立つ。
定理 06.2
素数
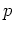
の巾
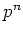
が与えられたとき、元の個数が
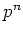
の体
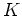
が存在する。
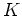
は同型を除いて一意的である。
系 06.1
任意の素数
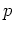
と任意の正の整数
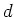
に対して、
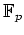
上の既約
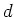
次式が
少なくとも一つ存在する。
定義 06.2
元の個数が
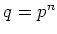
の体のことを
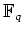
と書く。
問題 06.1
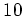
以上の素数
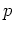
と
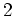
以上の整数
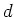
を各自で決めて、
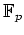
上既約かつモニックな多項式を二つ与え(
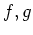
)、
![$ {\mathbb{F}}_p[X]/f(X){\mathbb{F}}_p[X]$](img23.png)
での
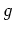
の根を書き下しなさい。
平成16年12月6日
![]()