


: この文書について...
代数学I特論要約 No.07
今日のテーマ

標数 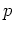 の体や、それを含む環には、面白い自己準同型が存在する。
の体や、それを含む環には、面白い自己準同型が存在する。
命題 07.1
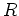
は(単位元をもつ可換)環で、
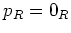
であるとする。(これは
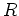
が
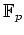
を含むと言っても同じ。)
このとき、
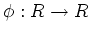 を
を
で定めると、
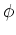
は
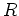
から
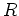
への環準同型になる。
(
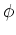
のことをフロベニウス準同型と呼ぶ。)
この命題を用いて先週やり残した部分を証明しておこう。
補題 07.1
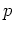
は素数であるとし、
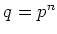
(
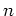
は正の整数)とする。
標数
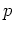
の任意の体
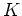
に対して、
は
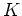
の(有限)部分体をなす。
さらに次のことの証明が残っていた。
ついでに多項式の性質の落ち穂拾いもしておこう。
命題 07.2
有限体上の既約な一変数多項式は重根をもたない。
平成16年11月15日
![]()
![]() の体や、それを含む環には、面白い自己準同型が存在する。
の体や、それを含む環には、面白い自己準同型が存在する。
![]() を
を