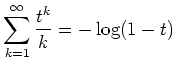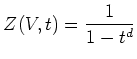今日のテーマ
![]()
以下 ![]() は素数であるとし、
は素数であるとし、 ![]() (
( ![]() は正の整数)であるとする。
は正の整数)であるとする。
![]() 個の変数
個の変数
![]() に関する
に関する
![]() 係数の
多項式
係数の
多項式
![]() が与えられているとき、 方程式系
が与えられているとき、 方程式系
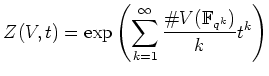
によって定義する。定義体
![]() を明示したい時は、
を明示したい時は、
![]() などとも書く。
などとも書く。
実際は右辺の級数は収束するのだが、 ここでは収束性は気にせずに「形式的べき級数」として扱うことにする。