代数学II 要約 No.1

有限群とその表現

有限群の定義は簡単なものであるが、その例を知らないと机上の空論になりかねない。 実は位数が 100以下ぐらいならば、手作業でも割りと簡単に与えられた 位数の有限群を全て決定することができる。

解析のキーになるのは シローの定理で、これは位数の素因数分解に対応して群を調べることを可能にする。

そのあと実際に群を作る際には行列などによる表現を 用いるのが楽である。

本講義ではその二つのことがらについて、 例を交えながら述べる。実際に与えられた位数の群がどのぐらいあるのか 見当がつくようになれば合格である。

なんと言っても簡単なのは巡回群である。 これは

$$C_n=\langle{a; a^n=e}\rangle$$

と書かれるもので、元の数(位数)が $n$ である。

これには、$a$ を $(1 2 3 \dots n)$ という巡回置換に対応することにより 置換による表現を与えることができる。

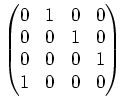
また、行列による表現を与えることもできる。$n=4$ ならば $a$ に

$$\begin{pmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \end{pmatrix}$$

を対応させるとよい。行列や置換で表現することにより、群が実際に存在することを 示すことができるとともに、計算による取扱いもやりやすくなるところが メリットである。

群の簡単な例としては他にも $n$ 個の元の置換全体からなる群($n$-次対称群) $\mathfrak{S}_n$ がある。例えば、 $\mathfrak{S}_3$ は位数 $6$ の 元である。$C_6$ も位数 $6$ であったから、同じ位数をもつ群が複数 あり得ることがわかる。

問題 1.1   4つの元 $\{1,2,3,4\}$ の置換全体からなる群 $\mathfrak{S}_4$ の元を 全て書き、 $\mathfrak{S}_4$ の位数はいくらか答えなさい。

問題 1.2   4つの元 $\{1,2,3,4\}$ の偶置換全体からなる群 $\mathfrak{A}_4$ の元を 全て書き、 $\mathfrak{S}_4$ の位数はいくらか答えなさい。