


: この文書について...
documentclass[12pt]amsart
usepackageeucal,amssymb
par
newedtheoremtheorem定理[section]newedtheoremnitheoremあまり重要でない定理[section]renewedcommandthenitheorem
newedtheoremrefpropPropositionrenewedcommandtherefprop
newedtheoremcorollary系[section]newedtheoremlemma補題[section]newedtheoremfact事実[section]newedtheoremproposition[theorem]命題newedtheoremaxAxiompar
theoremstyledefinition
newedtheoremdfn定義[section] newedtheoremexmp例[section] newedtheoremexample例[section]newedtheoremdefinition定義[section] newedtheoremq問題[section] newedtheoremexq例題[section] newedtheoremkeywd数学のキーワードpar
theoremstyleremark
newedtheoremrem注意[section]newedtheoremclaim[]renewedcommandtheclaim par
numberwithinequationsection
par
newedcommandtheoremref[1]Theorem ref#1
newedcommandsecref[1]Sref#1
newedcommandlemref[1]Lemma ref#1
par
newedcommandZmbox
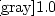 newedcommandQmbox
newedcommandQmbox
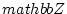 newedcommandRmbox
newedcommandRmbox
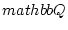 newedcommandNmbox
newedcommandNmbox
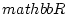 newedcommandImbox
newedcommandImbox
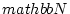 par
newedcommandLeg[2]mbox
par
newedcommandLeg[2]mbox
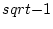 newedcommandFpmbox
newedcommandFpmbox
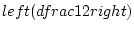 newedcommandkpekembox
newedcommandkpekembox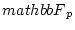 newedcommandbigzerolsmashhboxhuge 0
newedcommandbigzerousmashlower1.7exhboxhuge 0
par
begindocument
title[代数学II 要約 No.thistime ]代数学II 要約 No.thistime
par
quad
vskip -3pc
maketitle
par
setcountersectionthistime
par
今日のテーマ
par
fbox部分群、剰余群、剰余集合、ラグランジュの定理
par
今回から数回に渡って、復習の意味もこめて群論の初歩をたどってみよう。
但し足取りはかなり早い。代数Cや 代数I の段階では扱わなかった
かも知れない複雑な例も扱う場合があるから、注意すること。
par
まず、先週講義では触れたが要約には書かなかったので、群の定義を
書いておく。
begintheorem_type[definition][definition][section][definition][][]
newedcommandbigzerolsmashhboxhuge 0
newedcommandbigzerousmashlower1.7exhboxhuge 0
par
begindocument
title[代数学II 要約 No.thistime ]代数学II 要約 No.thistime
par
quad
vskip -3pc
maketitle
par
setcountersectionthistime
par
今日のテーマ
par
fbox部分群、剰余群、剰余集合、ラグランジュの定理
par
今回から数回に渡って、復習の意味もこめて群論の初歩をたどってみよう。
但し足取りはかなり早い。代数Cや 代数I の段階では扱わなかった
かも知れない複雑な例も扱う場合があるから、注意すること。
par
まず、先週講義では触れたが要約には書かなかったので、群の定義を
書いておく。
begintheorem_type[definition][definition][section][definition][][]
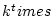 が群であるとは、
beginenumerate
setcounterenumi-1
renewedcommandlabelenumi(群arabicenumi)
item 演算
が群であるとは、
beginenumerate
setcounterenumi-1
renewedcommandlabelenumi(群arabicenumi)
item 演算
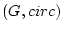 は写像である。つまり、
は写像である。つまり、
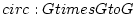 の元二つの組
の元二つの組 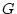 に対して
に対して 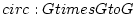 の元
の元
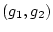 が
定まる。
item
が
定まる。
item 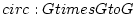 の演算
の演算 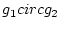 は結合律をみたす。
item
は結合律をみたす。
item 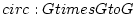 には単位元が存在する。
item
には単位元が存在する。
item 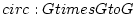 の各元には逆元が存在する。
endenumerate
の条件が満たされるときにいう。endtheorem_type
(演算
の各元には逆元が存在する。
endenumerate
の条件が満たされるときにいう。endtheorem_type
(演算 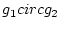 が何であるか話の流れから了解済みのときには、
が何であるか話の流れから了解済みのときには、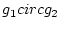 を
書かずに単に
を
書かずに単に 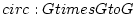 のことを群と呼ぶことも多い。)
群
のことを群と呼ぶことも多い。)
群 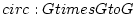 の元の個数のことを群の位数と呼び、
の元の個数のことを群の位数と呼び、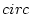 で書き表す。
par
群が与えられると、その部分群がどのようなものかを考えるのは
基本的である。部分群の定義は簡単で、
par
begintheorem_type[definition][definition][section][definition][][]
群
で書き表す。
par
群が与えられると、その部分群がどのようなものかを考えるのは
基本的である。部分群の定義は簡単で、
par
begintheorem_type[definition][definition][section][definition][][]
群 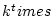 の部分群とは、
の部分群とは、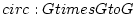 の部分集合
の部分集合 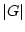 であって、
であって、
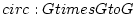 の演算
の演算 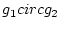 を制限することにより
を制限することにより 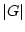 自身が群になっている
ときにいう。endtheorem_type
par
さて、群
自身が群になっている
ときにいう。endtheorem_type
par
さて、群 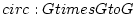 とその部分群
とその部分群 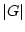 が定まったとき、剰余集合
が定まったとき、剰余集合 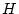 が
定義される。それは
が
定義される。それは 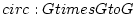 の「クラス分け」によって定まる。
par
begintheorem_type[definition][definition][section][definition][][]
の「クラス分け」によって定まる。
par
begintheorem_type[definition][definition][section][definition][][]
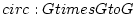 の部分群
の部分群 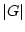 が与えられているとき、
が与えられているとき、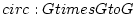 のクラス分けが次のように定まる。
vskip baselineskip
noindent
のクラス分けが次のように定まる。
vskip baselineskip
noindent
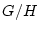 と
と 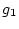 が同じクラス
が同じクラス 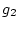
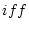 となる
となる 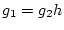 が存在する。
vskip baselineskip
beginenumerate
item このクラス分けによる
が存在する。
vskip baselineskip
beginenumerate
item このクラス分けによる 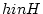 のクラスを
のクラスを 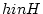 の
の 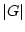 に関する左剰余類と呼ぶ。
item このクラス分けによるクラスの全体の集合を
に関する左剰余類と呼ぶ。
item このクラス分けによるクラスの全体の集合を 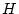 と書き、
と書き、
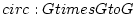 の
の 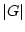 による左剰余集合と呼ぶ
endenumerate
parendtheorem_type
newpage
par
begintheorem_type[theorem][theorem][section][][][]
beginenumerate
item
による左剰余集合と呼ぶ
endenumerate
parendtheorem_type
newpage
par
begintheorem_type[theorem][theorem][section][][][]
beginenumerate
item 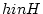 の
の 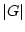 による左剰余類の全体は
と等しい。
item
による左剰余類の全体は
と等しい。
item 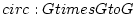 が有限群のとき、
(但し、
が有限群のとき、
(但し、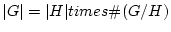 は集合
は集合 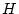 の元の個数)
item とくに、
の元の個数)
item とくに、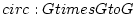 が有限群ならば、
が有限群ならば、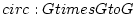 の部分群
の部分群 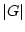 の位数(元の個数)
の位数(元の個数) 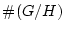 は
かならず
は
かならず 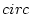 の約数である。(ラグランジュの定理)
endenumerate
parendtheorem_type
ラグランジュの定理(と、その特殊な場合として次回に扱うフェルマーの小定理)は、
位数が群にとって重要であることをしめす最初の例であろう。
par
begintheorem_type[q][q][section][definition][][]
群
の約数である。(ラグランジュの定理)
endenumerate
parendtheorem_type
ラグランジュの定理(と、その特殊な場合として次回に扱うフェルマーの小定理)は、
位数が群にとって重要であることをしめす最初の例であろう。
par
begintheorem_type[q][q][section][definition][][]
群
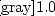 の元
の元 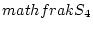 を
を
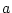 で定め、
とおく。このとき
で定め、
とおく。このとき 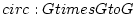 の
の 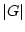 によるクラス分けの表を実際に書きなさい。endtheorem_type
par
begintheorem_type[q][q][section][definition][][]
群
によるクラス分けの表を実際に書きなさい。endtheorem_type
par
begintheorem_type[q][q][section][definition][][]
群
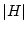 の部分群
の部分群 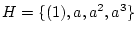 で、位数が
で、位数が 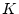 以上
以上 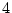 以下のもの
の例
(但し前問の
以下のもの
の例
(但し前問の 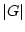 は当然除く)
を一つ見つけだし、その
は当然除く)
を一つ見つけだし、その 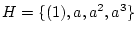 に対して
に対して 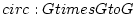 の
の 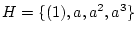 による
クラス分けの表を実際に書きなさい。endtheorem_type
par
enddocument
による
クラス分けの表を実際に書きなさい。endtheorem_type
par
enddocument
平成16年7月12日