


: この文書について...
代数学II 要約 No.3
今日のテーマ

一般に、写像
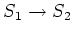 があればそれによって
があればそれによって 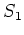 のクラスわけが定義される。
群の場合には群の構造を尊重した
群準同型写像を考えるのがよい。
今回は、群の演算を表すのに
のクラスわけが定義される。
群の場合には群の構造を尊重した
群準同型写像を考えるのがよい。
今回は、群の演算を表すのに 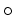 を用いる。
を用いる。
定義 3.1
群
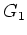
から群
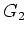
への写像
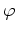
が群準同型写像であるとは、
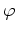
が演算を保つ。すなわち、
がすべての
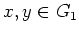
について成立するときにいう。
全単射群準同型のことを同型とよぶ。
補題 3.1
群準同型
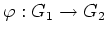
が与えられたとき、
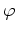
は
単位元、逆元を保つ。
群の準同型
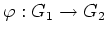 の核は単に
の核は単に 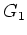 の部分群である
というだけではなく、特別な性質をもっている。
の部分群である
というだけではなく、特別な性質をもっている。
定義 3.2
群
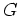
の部分群
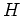
が
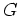
の正規部分群であるとは、
任意の
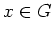
と 任意の
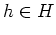
に対して
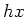
の
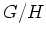
でのクラスが
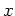
のクラスに等しいとき、
言い換えれば、ある
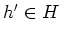
があって、
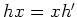
がなりたつときにいう。
命題 3.2
群
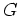
の正規部分群
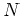
があたえられたとき、
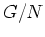
に
群の構造が、演算を
(
![$ [?]$](img28.png)
は
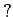
の
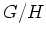
でのクラス)により定めることができる。
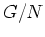
はこの演算について群をなす。
例 3.1
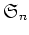
から
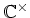
への写像
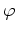
を
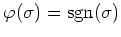
$&sigma#sigma;$ の 符号
で定義すると、
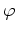
は群の準同型になる。
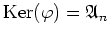
,
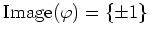
.
問題 3.1
群
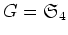
の元のうち、
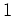
を動かさないようなものの全体を
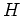
とおく。
すなわち
とおく。このとき
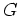
の
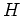
によるクラス分けの表を実際に書き、つぎに
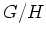
に演算を
(
![$ [?]$](img28.png)
は
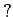
の
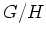
でのクラス。)
で定めようとしてもこれはうまく定義されないことを示しなさい。
すなわち、
![$ [x_1]=[x_2]$](img41.png)
かつ
![$ [y_1]=[y_2]$](img42.png)
であるにもかかわらず、
![% latex2html id marker 985
$ [x_1 y_1] \neq [x_2 y_2]$](img43.png)
であるような
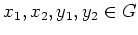
の例を挙げなさい。
問題 3.2
群
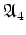
の正規部分群
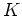
で、自明でないもの(つまり、
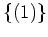
でも
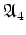
でもないものの例を挙げよ。
平成16年4月21日
![]()
![]() があればそれによって
があればそれによって ![]() のクラスわけが定義される。
群の場合には群の構造を尊重した
群準同型写像を考えるのがよい。
今回は、群の演算を表すのに
のクラスわけが定義される。
群の場合には群の構造を尊重した
群準同型写像を考えるのがよい。
今回は、群の演算を表すのに ![]() を用いる。
を用いる。
![]() の核は単に
の核は単に ![]() の部分群である
というだけではなく、特別な性質をもっている。
の部分群である
というだけではなく、特別な性質をもっている。