代数学II 要約 No.5

今日のテーマ

群 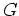$G$ には剰余類によるクラス分け以外にも、重要なクラス分けが存在する。 その一つが共役類によるクラス分けである。

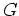
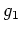
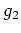
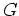
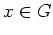
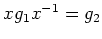
定義 5.1   群 $G$ の元 $g_1$ と $g_2$ とが $G$ のなかで共役であるとは、 ある $x\in G$ があって、 $x g_1 x^{-1}=g_2$ が成り立つときにいう。

剰余類によるクラス分けと違って、今度は各クラスの人数はバラバラである。 さしあたってすぐ分かるのは

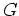
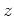
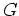
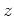
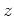
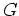
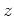
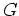
補題 5.1   $G$ の元 $z$ と $G$ のなかで共役なものが $z$ しかない(つまり共役類での クラス分けで一人ぼっちになる)には、 $z$ が $G$ の中心元であること (すなわち $z$ は $G$ のどの元とも可換であること) が必要十分である。

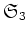
例 5.1   $\mathfrak{S}_3$ をクラス分けすると、

• $(1)$ のクラス (1名からなるクラス)
• $(1 \ 2)$ のクラス (3名からなるクラス)
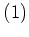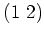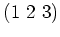• $(1 \ 2 \ 3)$ のクラス (2名からなるクラス)

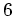
の三つに分かれる。もちろん、全体の人数は $6$ であるから、

$$6=1+3+2$$

という等式が成り立つ。このように、共役類のクラス構成員の人数の総和と 群の位数とが一致することを表現する式を類等式と呼ぶ。

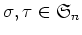
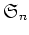
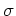
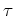
命題 5.1   置換 $\sigma, \tau \in \mathfrak{S}_n$ が $\mathfrak{S}_n$ のなかで 共役なのは、$\sigma$ の「文字の入れ換え」によって $\tau$ が得られるときで、 その時に限る。

上の命題は 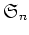$\mathfrak{S}_n$ のなかでの共役を言っていることに十分注意すること。

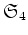
問題 5.1   群 $\mathfrak{S}_4$ の類等式を書きなさい。

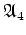
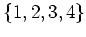
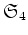
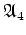
問題 5.2   群 $\mathfrak{A}_4$ ( $\{1,2,3,4\}$ の偶置換全体のなす群)の類等式を書きなさい。 ( $\mathfrak{S}_4$ のなかで共役であっても $\mathfrak{A}_4$ の中で共役とは 限らないことに十分注意すること。)