


: この文書について...
代数学II 要約 No.9
今日のテーマ
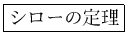
一般に、有限群 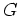 の部分群
の部分群 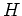 が与えられたとき、
が与えられたとき、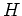 の位数は
の位数は
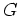 の位数の約数であった。(ラグランジュの定理)
の位数の約数であった。(ラグランジュの定理)
この逆は正しくない。つまり、
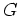 の位数の約数が与えられても、
の位数の約数が与えられても、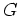 の部分群で、ちょうどその位数の
ものがあるとは、一般には限らない。しかし、特殊な場合に限っては
大丈夫なことがある。
の部分群で、ちょうどその位数の
ものがあるとは、一般には限らない。しかし、特殊な場合に限っては
大丈夫なことがある。
補題 9.1
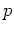
-群
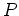
の位数
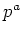
の任意の約数
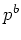
(
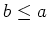
) にたいして、
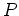
の部分群
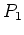
で、位数がちょうど
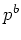
であるものが存在する。
系 9.1
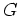
の位数が
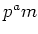
(
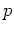
は素数、
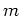
と
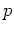
とは互いに素)であるとき、
任意の自然数
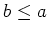
に対して、
位数
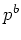
の
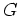
の部分群が存在する。
問題 9.1
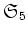
の
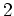
-シロー群、
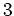
-シロー群の例をそれぞれ一つづつ挙げなさい。
平成16年6月14日
![]()
![]() の部分群
の部分群 ![]() が与えられたとき、
が与えられたとき、![]() の位数は
の位数は
![]() の位数の約数であった。(ラグランジュの定理)
の位数の約数であった。(ラグランジュの定理)
![]() の位数の約数が与えられても、
の位数の約数が与えられても、![]() の部分群で、ちょうどその位数の
ものがあるとは、一般には限らない。しかし、特殊な場合に限っては
大丈夫なことがある。
の部分群で、ちょうどその位数の
ものがあるとは、一般には限らない。しかし、特殊な場合に限っては
大丈夫なことがある。