


: この文書について...
代数学II 要約 No.10
今日のテーマ

前回は、この定理の(1)の部分を証明したが、少し分かりにくかったかも知れぬ。
まず、定理の主張から説明しておこう。
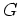 の位数
の位数 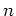 を
を 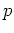 で割れるだけ割って、
で割れるだけ割って、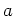 回で割れなくなったとする。
例えば、
回で割れなくなったとする。
例えば、 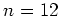 で
で 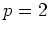 なら、
なら、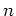 は
は 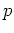 で
で 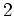 回割れて、
回割れて、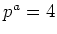 という具合である。このとき、
という具合である。このとき、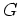 の部分群で、
位数
の部分群で、
位数 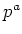 のものが存在するということである。
のものが存在するということである。
例 10.1
- 位数
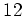 の群には
位数
の群には
位数 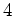 の部分群 (
の部分群 (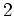 -シロー群)と 位数
-シロー群)と 位数 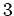 の部分群
(
の部分群
(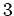 -シロー群)が必ず存在する。
-シロー群)が必ず存在する。
- 位数
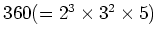 の群には
位数
の群には
位数 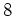 の部分群 (
の部分群 (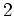 -シロー群)と 位数
-シロー群)と 位数 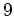 の部分群
(
の部分群
(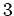 -シロー群)、位数
-シロー群)、位数 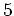 の部分群が必ず存在する。
の部分群が必ず存在する。
そのようなシロー群は、どのように見つければよいのか、これが前回の証明であって、
- もし
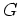 の部分群
の部分群 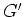 で、
で、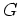 より真に小さく、なおかつ
より真に小さく、なおかつ 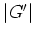 が
が 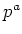 の倍数であるようなものを見つけることができれば、話の対象を
の倍数であるようなものを見つけることができれば、話の対象を 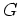 から
から 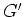 に
移すことができる。(
に
移すことができる。(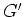 の部分群は
の部分群は 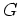 の部分群でもあるからである。)
の部分群でもあるからである。)
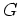 の部分群
の部分群 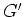 の例としては、
の例としては、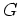 のいろいろな元
のいろいろな元 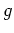 に対する
中心化群
に対する
中心化群 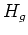 を 考えることができる。
を 考えることができる。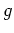 をいろいろとることで、
かなりの確率でそのような
をいろいろとることで、
かなりの確率でそのような 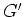 を見つけることができるだろう。
を見つけることができるだろう。
- もし不幸にもそのようなものが一つもなかったとするしよう。このときは
類等式を利用して、
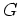 の中心
の中心 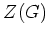 は
は 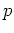 の倍数で
なければならないことが分かる。ところが
の倍数で
なければならないことが分かる。ところが 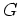 の中心が大きければ、
の中心が大きければ、
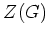 の部分群
の部分群 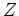 を適当にとって
それで剰余群を作ることにより
を適当にとって
それで剰余群を作ることにより 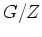 と
と 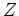 の二つに話を分けて
やはり話を位数が
の二つに話を分けて
やはり話を位数が 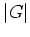 より小さな群に帰着させることができるのである。
より小さな群に帰着させることができるのである。
最後の部分は、具体的には次のような補題を証明すればよい。
補題 10.1
- 可換群
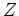 の位数が素数
の位数が素数 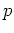 で割れるならば、
で割れるならば、 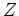 の元
の元 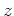 で、
位数がちょうど
で、
位数がちょうど 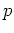 のものが存在する。
のものが存在する。
- 群
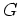 の中心
の中心 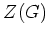 の部分群
の部分群 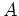 は、必ず
は、必ず 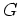 の正規部分群である。
の正規部分群である。
問題 10.1
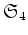
の 2-シロー群、 3-シロー群の個数はそれぞれいくらか。
問題 10.2
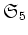
の 2-シロー群、 3-シロー群、5-シロー群の個数はそれぞれいくらか。
平成16年6月21日
![]()
![]() の位数
の位数 ![]() を
を ![]() で割れるだけ割って、
で割れるだけ割って、![]() 回で割れなくなったとする。
例えば、
回で割れなくなったとする。
例えば、 ![]() で
で ![]() なら、
なら、![]() は
は ![]() で
で ![]() 回割れて、
回割れて、![]() という具合である。このとき、
という具合である。このとき、![]() の部分群で、
位数
の部分群で、
位数 ![]() のものが存在するということである。
のものが存在するということである。