


: この文書について...
代数学II 要約 No.11
今日のテーマ

シローの定理をもちいると、例えば次の結果を証明できる。
シローの定理とは違うが、次のことにも注意しておこう。
補題 11.1
有限群
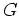
の部分群
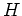
が与えられたとき、
は、
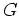
の部分群であり、
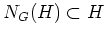
である。
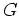
の部分群で
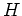
と共役なものの個数
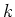
は、
![$ [G:N_G(H)]$](img14.png)
にひとしい。
とくに、
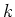
は
![$ [G:H]$](img15.png)
の約数である。
系 11.1
有限群
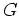
の位数が
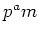
(
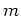
は
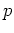
で割り切れない)であるとする。
このとき、
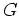
の
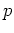
-シロー群の個数
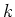
は
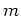
の約数である。
シローの定理により 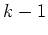 は
は 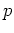 の倍数であることに注目すると、
上のこととあわせて
の倍数であることに注目すると、
上のこととあわせて 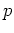 -シロー群の数について強い制限がつくことが分かる。
-シロー群の数について強い制限がつくことが分かる。
次の二つの補題も位数が低い群を調べる際には有効である。
補題 11.2
群
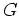
の素数位数の部分群
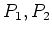
があるとき、
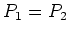
または
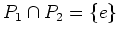
のどちらかが成り立つ。
補題 11.3
有限群
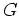
の位数
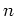
が素数
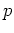
でただ一度だけ割れるとする。
すなわち、し、
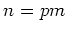
で、
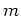
は
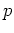
で割れないとする。
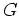
の
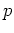
-シロー群の個数を
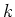
個とすると、
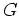
の元で、位数が
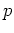
のものはちょうど
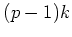
個である。
問題 11.1
位数
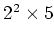
の群
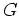
には必ず自明でない正規部分群
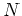
が
存在することを示しなさい。
問題 11.2
位数
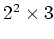
の群
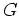
の
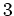
-シロー群か
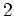
-シロー群のいずれかは正規部分群である
ことを示しなさい。
(どちらの場合も起こり得る。)
平成16年6月25日
![]()
![]() は
は ![]() の倍数であることに注目すると、
上のこととあわせて
の倍数であることに注目すると、
上のこととあわせて ![]() -シロー群の数について強い制限がつくことが分かる。
-シロー群の数について強い制限がつくことが分かる。