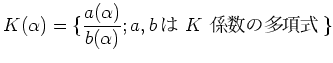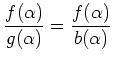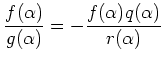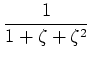Next: About this document ...
代数学III 要約 No.2
今日のテーマ

定義 2.1
体
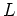
の部分集合
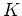
が
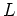
の部分体であるとは、
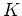
自身が
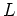
の演算で体になっているときに言う。
定義 2.2 (体に元を付け加えてできる
体)
体
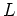
と、その部分体
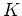
, および
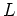
の元
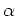
が
与えられているとする。
このとき、
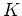
と
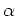
とを含む
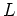
の部分体のうち最小のものを
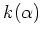
(
丸括弧に注意)
と書き、
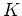
に
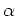
を付け加えてできる体と呼ぶ。
定義 2.3
体
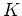
は体
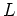
の部分体であるとする。
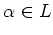
が
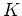
上代数方程式
を満足するとき、
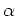
は
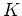
上代数的であると呼ぶ。
命題 2.1
体 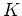 が体
が体 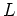 の部分体であって、
の部分体であって、
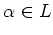 が
が 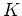 上代数的であれば、
上代数的であれば、
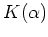 の任意の元は
の任意の元は 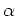 の
の 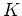 係数の多項式で書くことができる。
係数の多項式で書くことができる。
上の命題の証明はユークリッドの互除法を用いるのがもっとも普通であるが、
ここではそれとほぼ等価な次の方法を採ろう。
問題 2.1
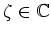
は
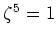
を満たすような複素数であるとする。このとき、
を
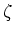
の有理数係数の多項式に直しなさい。
2006-10-12
![]()