: この文書について...
代数学演習 I 問題 No.2

注意
これからは、とくにことわらない限り、単位元をもつ環のみを扱う。「環」といえば、
単位元を持つ環と解釈していただきたい。(単位元の存在がとくに重要な時には、
一応ことわる。)ただし、積が可換であるとはまだ仮定しない。
問題 2.1
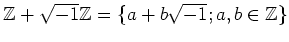
は環となることを示しなさい。(
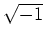
は虚数単位をあらわす記号です。)
問題 2.2
単位元
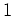
を持つ環

の元
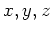
にたいして、
| |
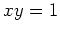 (すなわち (すなわち 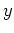 は は 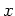 の右逆元である。) の右逆元である。) |
|
| |
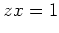 (すなわち (すなわち 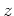 は は 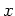 の左逆元である。) の左逆元である。) |
|
が成り立つとき、
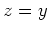
であって、
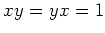
(すなわち $y(=z)$ は $x$ の逆元である)
が成り立つことを示しなさい。
定義 2.1
単位元の存在する環

において、逆元が存在するような元のことを、

の可逆元とか、単元、あるいは単数といいます。
問題 2.3

を単位元の存在する環とします。

の可逆元全体
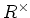
は群をなすことを示しなさい。
定義 2.2
前問の
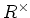
のことを

の単数群といいます。
問題 2.4
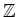
の単数群を求めなさい。
問題 2.5
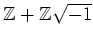
の単数群を求めなさい。
上の条件のうち、(1)が本質的部分であり、(2) は冒頭で述べた注意に沿うための
技術的条件である。ただし、(2)をぬかしてしまうと理論は見かけ上かなり違った
形になるので単位元のない環を扱う時(がもしあればその時)には注意が必要である。
問題 2.8
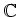
の部分環
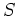
が、
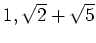
を元として持っているとします。
この時、
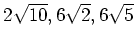
も
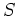
の元であることを示しなさい。
定義 2.4
単位元をもつ可換環

が
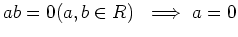
or
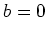
を満たす時、

を整域とよぶ
問題 2.9
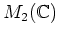
の部分集合
は加法、減法、乗法について閉じていることを示し、
これが単位元をもつ可換環であることを言いなさい。
さらに、この環は整域ではないことを示しなさい。
問題 2.10

が可換環
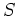
の部分環であるとき、

も可換環になり、さらに
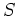
が整域であれば

も整域であることを示しなさい。
問題 2.11
実数を成分に持つ
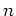
-次正方行列のなす集合
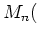

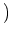
は通常の算法によって環になることを定義に沿って説明しなさい。
問題 2.13
環

の元
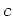
がある正整数
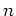
により
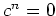
となるとき、
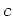
を巾零元と言います。もし

が単位元
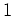
を持ち、
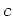
が

の巾零元とするならば、
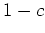
は

の単元となることを示しなさい。
問題 2.14
有限個の元しか持たない整域は、体となることを示しなさい。
問題 2.15
有理数体
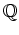
を部分環として含むような
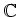
の部分環

(つまり、
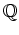
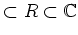
)
が
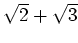
を元として含むとき、
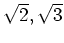
も

の元であることを示しなさい。
問題 2.16
有理数体
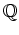
を部分環として含むような
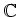
の部分環

が
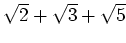
を元として含むとき、
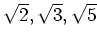
も

の元であることを示しなさい。
問題 2.17
有理数体
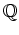
を部分環として含むような
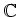
の部分環

について、次の二つの条件は同値であることを
示しなさい。
-
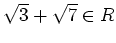 .
.
-
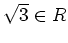 かつ
かつ
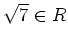 .
.
問題 2.18
前問で、

が
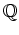
を部分環として含む、という条件を
外しても同様のことが言えるだろうか。
正しいなら証明し、間違っているなら反例を
あげなさい。
問題 2.19
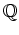
を部分環として含むような
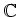
の部分環

で、
体でないようなものは存在するだろうか。
(難問である。この問題については大枠が示せれば良い。)
問題 2.20
-
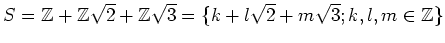 は
は
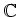 の部分環だろうか?
の部分環だろうか?
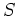 を含む、
を含む、
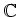 の部分環で、最小のもの(つまり、
の部分環で、最小のもの(つまり、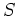 で
生成される
で
生成される
 の部分環はなにか?
の部分環はなにか?



: この文書について...
平成17年10月17日
![]()