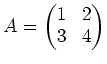: この文書について...
代数学 I No.2要約
補題 2.1
単位元を持つ環
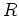
と、その部分集合
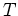
が与えられていたとする。このとき、
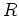
の部分環
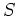
で、
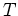
で環として生成されるものがただ一つ存在する。
(
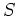
のことを
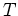
で生成される
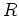
の部分環といい、
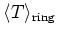
と書く。
注意
「部分環」の定義により、
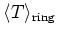 は(
は(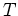 が何であっても)
常に
が何であっても)
常に 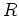 の単位元
の単位元 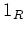 を元としてもつ。
しかし、単位元の存在を意識しておくために、以下では
始めから
を元としてもつ。
しかし、単位元の存在を意識しておくために、以下では
始めから 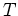 には
には 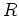 の単位元
の単位元 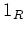 が入ったものだけを考えることにする。
が入ったものだけを考えることにする。
上の補題の証明の途中で、次の補題が必要になるので、ここに掲げておく。
補題 2.2 (「任意個数の部分環の共通部分はまた部分環である。」)
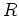
は環であるとし、
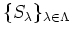
は
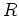
の部分環の族であったとする。このとき、
もまた
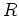
の部分環になる。
実際には、生成される部分環には次のパターンのものがよく使われる。
定義 2.2
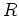
を環、
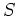
をその部分環とする。
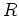
の元
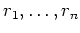
が与えられたとき、
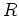
の部分集合
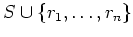
で生成される部分環を、
![$ S[r_1,\dots,r_n]$](img18.png)
と書き、
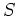
上
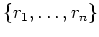
で生成された環とよぶ。
この記法によれば、上の例の4.,5. はそれぞれ次のように書ける。
このように、
![$ S[r_1,\dots,r_n]$](img18.png) が実際にはどのような元を
もつのか決定することも基本的で、重要である。それは通常
次の手順で行う。
が実際にはどのような元を
もつのか決定することも基本的で、重要である。それは通常
次の手順で行う。
-
![$ S[r_1,\dots,r_n]$](img18.png) の候補
の候補 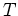 を探す。
を探す。
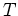 は
は
![$ S[r_1,\dots,r_n]$](img18.png) を部分集合として含むことを証明する。
を部分集合として含むことを証明する。
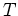 は
は 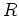 の部分集合であることを証明する。
の部分集合であることを証明する。
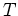 の元は
の元は 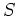 と、
と、
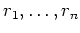 から構成し得ることを
証明する。言い換えると、
から構成し得ることを
証明する。言い換えると、
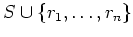 を部分集合として含む
を部分集合として含む 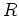 の部分環は、必ず
の部分環は、必ず
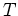 を含むことを証明する。
を含むことを証明する。
定義 2.3
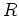
は環であるとする。このとき、
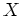
を変数とする
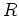
係数の一変数多項式の全体
は環をなす。(足し算、かけ算は通常のものを考える。)
この環を
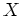
を変数とする
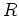
上の一変数多項式環という。
定理 2.1
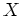
を変数とする
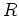
上の一変数多項式環は、
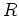
と、
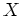
とで生成される。
(したがって、これからは
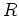
上の一変数多項式環のことを
![$ R[X]$](img30.png)
と書く。)
注意
代数I の範囲では他に
![$ {\mathbb{C}}[X],$](img31.png)
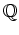
![$ [X]$](img32.png) 等が重要になる。
(
等が重要になる。
(
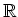 ,
,
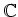 ,
,
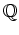 は全て体である。すなわち積は可換であり、
0 以外の各元は逆元を持つ。)
は全て体である。すなわち積は可換であり、
0 以外の各元は逆元を持つ。)
※レポート問題
つぎのうち一問を選択して解きなさい。
(期限:次の講義の終了時まで。)
- (I).
-
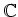 の部分環
の部分環 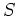 が、
が、
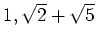 を元として持っているとする。
この時、
を元として持っているとする。
この時、
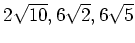 も
も 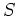 の元であることを示しなさい。
の元であることを示しなさい。
- (II).
-
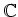 の、
の、
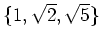 で生成される部分環は、
であることを示しなさい。
で生成される部分環は、
であることを示しなさい。
- (III).
-
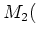
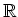
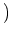 の、
の、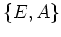 で生成される部分環を求めなさい。
ただし、
で生成される部分環を求めなさい。
ただし、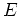 は単位行列、
は単位行列、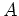 は次のような二次行列とします。
は次のような二次行列とします。



: この文書について...
平成17年10月17日
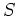 は
は 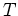 を部分集合として含む。
を部分集合として含む。
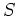 は
は 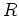 の部分環である。
の部分環である。
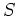 は 1.,2.を満たす最小のものである。
は 1.,2.を満たす最小のものである。
![]() は(
は(![]() が何であっても)
常に
が何であっても)
常に ![]() の単位元
の単位元 ![]() を元としてもつ。
しかし、単位元の存在を意識しておくために、以下では
始めから
を元としてもつ。
しかし、単位元の存在を意識しておくために、以下では
始めから ![]() には
には ![]() の単位元
の単位元 ![]() が入ったものだけを考えることにする。
が入ったものだけを考えることにする。
![]() が実際にはどのような元を
もつのか決定することも基本的で、重要である。それは通常
次の手順で行う。
が実際にはどのような元を
もつのか決定することも基本的で、重要である。それは通常
次の手順で行う。
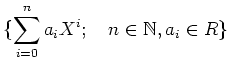
![% latex2html id marker 1268
$\displaystyle \{\sum_{i=0}^n a_iX^i ;\quad n\in \mathbb{N}, a_i \in R\}
=\langle R\cup \{X\} \rangle_{\text{ring}}=R[X]
$](img29.png)
![]()
![]()
![]() 等が重要になる。
(
等が重要になる。
(
![]() ,
,
![]() ,
,
![]() は全て体である。すなわち積は可換であり、
0 以外の各元は逆元を持つ。)
は全て体である。すなわち積は可換であり、
0 以外の各元は逆元を持つ。)