


: この文書について...
1=3
1 by -1
代数学 I No.3要約
 イデアルとそれによる剰余環、環
イデアルとそれによる剰余環、環
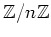
環をイデアルで割ることにより、新しい環を作ることが出来る。
これは、群を正規部分群で割る操作に似ている。
とくに、
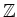 を
を
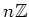 で割った環は重要である。
で割った環は重要である。
補題 3.1
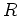
が単位元をもつ環であるとし、
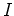
をそのイデアルとする。
このとき、
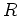 に同値関係
に同値関係 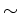 が、次のようにして決まる。
が、次のようにして決まる。
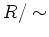 に、足し算を次のようにして入れる。
に、足し算を次のようにして入れる。
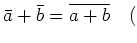
$?$ は $?$ の $&sim#sim;$ に関する
クラスを表す。
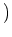
この足し算はうまく定義されていて、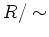 はこの足し算について可換群になる。
はこの足し算について可換群になる。
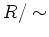 に、かけ算を次のようにして入れる。
このかけ算はうまく定義されていて、
に、かけ算を次のようにして入れる。
このかけ算はうまく定義されていて、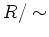 はこのかけ算について半群になる。
はこのかけ算について半群になる。
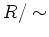 は上で定義された足し算、かけざんに関し環をなす。
しかも、この環は単位元
は上で定義された足し算、かけざんに関し環をなす。
しかも、この環は単位元 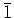 を持つ。
を持つ。
定義 3.2
上の補題の仮定のもとで、
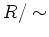
に上のような足し算、かけ算を入れて
環にしたものを
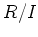
と書き、
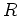
の
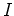
による剰余環と呼ぶ。
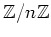 は、
は、
![$ {\mbox{${\mathbb{Z}}$}},{\mathbb{C}}[X]$](img27.png) の次に重要な環の例である。環についての議論が
正しいかどうかはこれらの環についてまずチェックしてみるのがよい。
の次に重要な環の例である。環についての議論が
正しいかどうかはこれらの環についてまずチェックしてみるのがよい。
注意
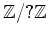 においては、単に
においては、単に 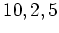 と書く代わりに、
と書く代わりに、
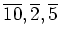 あるいは
あるいは
![$ [10],[2],[5]$](img39.png) 等の記号を使って通常の数と区別することが多い。
上の補題では、通常の感覚との違いを浮き出させるために、
わざと
等の記号を使って通常の数と区別することが多い。
上の補題では、通常の感覚との違いを浮き出させるために、
わざと 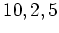 等と書いた。上のような例があるので、
一般の環
等と書いた。上のような例があるので、
一般の環 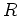 の元として例えば
の元として例えば
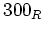 (または略して 単に
(または略して 単に 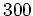 )を考える時には、
これが 0 かも知れない
ということを常に意識しておく必要がある。
)を考える時には、
これが 0 かも知れない
ということを常に意識しておく必要がある。
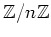 の性質は
の性質は 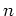 が素数かどうかによって少し違って来る。
それを説明するために、まず言葉を二つ用意する。
が素数かどうかによって少し違って来る。
それを説明するために、まず言葉を二つ用意する。
実は、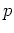 が素数ならば、
が素数ならば、
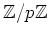 は体であることがわかる。それには
次の補題を使えばよい。
は体であることがわかる。それには
次の補題を使えばよい。
補題 3.4
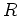
が整域で、かつ
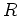
の元の数
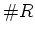
は有限であるとする。
このとき、
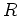
は体である。とくに、
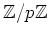
は体である。
系 3.1
素数
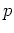
と、
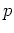
で割り切れない整数
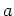
とに対し、
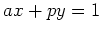
となる整数
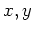
が存在する。
※レポート問題
つぎのうち一問を選択して解きなさい。
(期限:次の講義の終了時まで。)
- (I).
- (i)
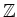 の元
の元 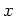 で、
で、
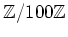 の中で考えると
の中で考えると
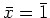 が成り立つ例を 5つあげなさい。(オリジナルであること:
数はたくさんあるんだからケチケチしないで
大きな数字をあげれば他の人と重ならないでしょう。)
(ii)
が成り立つ例を 5つあげなさい。(オリジナルであること:
数はたくさんあるんだからケチケチしないで
大きな数字をあげれば他の人と重ならないでしょう。)
(ii)
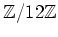 の零因子をすべてあげ、それらが零因子であることを実際に
示しなさい。
の零因子をすべてあげ、それらが零因子であることを実際に
示しなさい。
- (II).
-
![$ R={\mbox{${\mathbb{Z}}$}}[X]/(2,X^2+X+1)$](img56.png) の元(4つある)をすべて書き、実際にそれらで
の元(4つある)をすべて書き、実際にそれらで 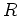 の
元がつきていることを示しなさい。
の
元がつきていることを示しなさい。
- (III).
- (II) の環
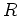 は体であることを示しなさい。
は体であることを示しなさい。



: この文書について...
平成17年11月17日
![]() イデアルとそれによる剰余環、環
イデアルとそれによる剰余環、環
![]()
![]() を
を
![]() で割った環は重要である。
で割った環は重要である。
![]() は、
は、
![]() の次に重要な環の例である。環についての議論が
正しいかどうかはこれらの環についてまずチェックしてみるのがよい。
の次に重要な環の例である。環についての議論が
正しいかどうかはこれらの環についてまずチェックしてみるのがよい。
![]() においては、単に
においては、単に ![]() と書く代わりに、
と書く代わりに、
![]() あるいは
あるいは
![]() 等の記号を使って通常の数と区別することが多い。
上の補題では、通常の感覚との違いを浮き出させるために、
わざと
等の記号を使って通常の数と区別することが多い。
上の補題では、通常の感覚との違いを浮き出させるために、
わざと ![]() 等と書いた。上のような例があるので、
一般の環
等と書いた。上のような例があるので、
一般の環 ![]() の元として例えば
の元として例えば
![]() (または略して 単に
(または略して 単に ![]() )を考える時には、
これが 0 かも知れない
ということを常に意識しておく必要がある。
)を考える時には、
これが 0 かも知れない
ということを常に意識しておく必要がある。
![]() の性質は
の性質は ![]() が素数かどうかによって少し違って来る。
それを説明するために、まず言葉を二つ用意する。
が素数かどうかによって少し違って来る。
それを説明するために、まず言葉を二つ用意する。
![]() が素数ならば、
が素数ならば、
![]() は体であることがわかる。それには
次の補題を使えばよい。
は体であることがわかる。それには
次の補題を使えばよい。