


: この文書について...
代数学 I No.11要約
 《剰余環、準同型定理の復習》
《剰余環、準同型定理の復習》
環
![$ R={\mbox{${\mathbb{Z}}$}}[X]/(X^2-3)$](img2.png) において、
において、
![$ X\in {\mbox{${\mathbb{Z}}$}}[X]$](img3.png) の
の 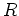 でのクラスを
でのクラスを
![$ [X]$](img5.png) と書くと、
と書くと、![$ [X]^2-3=0$](img6.png) . すなわち、
. すなわち、
![$ [X]$](img5.png) は
は 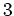 の平方根の役割を果たす。
の平方根の役割を果たす。
このことをまとめたのが、次の補題である。
同様に、
が成り立つ。これらの補題の証明には、準同型定理を使うのが便利である。
補題 11.3
![$ R={\mathbb{C}}[X]/(X^{10})$](img10.png)
において、
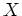
のクラスを
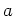
とおくと、
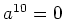
が成り立つ。とくに、
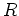
において
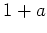
は可逆であり、
その逆元は
である。
補題 11.4
![$ R={\mbox{${\mathbb{Z}}$}}[X]/(X^2-4X+2)$](img16.png)
において、
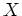
のクラスを
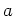
とおくと、
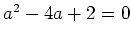
が成り立つ。このことから、
![% latex2html id marker 805
$ R\cong {\mbox{${\mathbb{Z}}$}}[\sqrt{2}]$](img18.png)
がわかる。
※レポート問題
つぎのうち一問を選択して解きなさい。
(期限:次の講義の終了時まで。)
- (I).
-
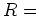
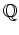
![$ [X]/(X^2+X+1)$](img21.png) において、元
において、元 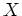 の
の 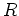 でのクラスを
でのクラスを 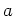 と書いたとき、
と書いたとき、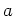 の満足する方程式をみつけて、
であることを証明しなさい。
の満足する方程式をみつけて、
であることを証明しなさい。
平成18年1月17日
![]() 《剰余環、準同型定理の復習》
《剰余環、準同型定理の復習》
![]() において、
において、
![]() の
の ![]() でのクラスを
でのクラスを
![]() と書くと、
と書くと、![]() . すなわち、
. すなわち、
![]() は
は ![]() の平方根の役割を果たす。
の平方根の役割を果たす。