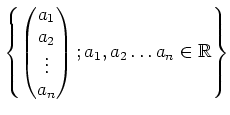

Next: About this document ...
Up: 代数学 C(コア) 演習問題 No.1
Previous: 代数学 C(コア) 演習問題 No.1
問題 1.1
群の定義は、簡単に言うと
(0)掛け算が定義されていて、
- その掛け算は結合法則を満たす。
- 更に単位元
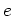 が存在し、
が存在し、
- その上割り算もできる。
というものです。
これを正確に集合の言葉を用いて述べなさい。
(適当な本を調べてノート/黒板に書きなさい。)
例 1.1
群
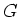
の「掛け算」というのは集合の言葉を使えば単に写像
のことです。(普通の意味の「掛け算」とは限らない事に注意しましょう。
たとえば
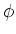
が実際には「足し算」の時もあります。
(下の問題1.2 を参照の事。)
その手の混乱を避けるために、
群の掛け算の事を「乗法」とか「積」とか難しい言葉で言うことが多いです。)
問題 1.2
いま、
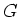
として整数全体のなす集合
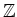
をとり、乗法
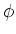
を
で定義すれば、
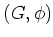
は群の公理を満たす事を確かめなさい。
次に、
と置いたときは
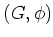
それぞれ群になるかどうか答えなさい。(こういう聞き方のときには当然理由を述べて答えてくださる事を期待してます。更に公理のうちどの部分は満足されているかも考えてください。以下も同様。)
問題 1.3
前の問題で、
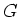
として
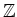
の代わりに
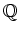
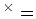
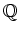
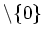
(有理数の全体から 0
のみを除いた集合)を採ったときにはどうなりますか?
問題 1.4
0
以下の整数の全体
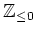
は足し算について群になっていますか?
かけ算についてはどうですか?
問題 1.5
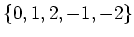
は足し算に関して群になっていません。なぜですか?
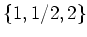
は掛け算に関して群になっていますか?
問題 1.6
有理数を要素とする
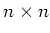
-行列全体の集合
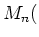
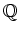
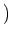
について、乗法を行列の通常の意味の積で定義します。この集合は群の公理を満たしますか?
問題 1.7
集合
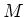
から
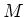
への写像全体のなす集合
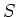
を考えます。この集合に乗法
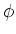
を「写像の合成」即ち
で定義できます。これを確かめなさい。
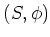
は群になりますか?
問題 1.8
次の各々のものは、写像になっていますか?それらは全射、単射、全単射ですか?
-
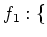 $3$ の倍数
$3$ の倍数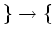 $6$ の倍数
$6$ の倍数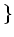 を
を
で定義したもの。
-
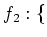 $3$ の倍数
$3$ の倍数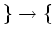 $6$ の倍数
$6$ の倍数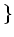 を
を
で定義したもの。
-
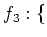 $2$ の倍数
$2$ の倍数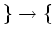 $8$ の倍数
$8$ の倍数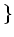 を
を
で定義したもの。
-
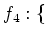 $2$ の倍数
$2$ の倍数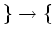 $8$ の倍数
$8$ の倍数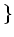 を
を
で定義したもの。
注意
数学では、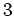 の倍数といえば、負のものや 0
も含みます。
また、「
の倍数といえば、負のものや 0
も含みます。
また、「
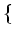 $3$ の倍数
$3$ の倍数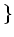 」
というのは
」
というのは 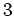 の倍数全体という意味です。
の倍数全体という意味です。
この集合を普通
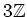 と書きます。
と書きます。
問題 1.9
複素数全体の集合を
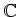
と書きます。
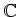
から
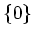
を除いた集合
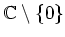
はかけ算に関して群をなすことを示しなさい。
特に
の逆元を求めなさい。
問題 1.10
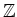
に次のような演算をいれたものは群であることを示しなさい。
問題 1.11
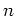
次元実ベクトル空間
は足し算に関して群になるかどうか、答えなさい。
定義 1.1 (確認)
群
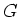
の部分集合
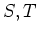
について、その「積」
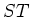
が、
で定義されます。
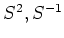
等についても同様です。
問題 1.12
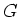
を0
以外の有理数全体に乗法を通常の掛け算で定義した群とします。
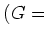
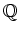
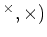
。この時、
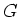
の部分集合
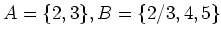
について、
を計算しなさい。
(★)
http://www.math.kochi-u.ac.jp/docky/kogi/
にアクセスすると、このプリント自体がとれますので、
正規の時間にとり損なった人は、各自そこからとってください。


Next: About this document ...
Up: 代数学 C(コア) 演習問題 No.1
Previous: 代数学 C(コア) 演習問題 No.1
2006-04-11
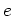 が存在し、
が存在し、
![]() の倍数といえば、負のものや 0
も含みます。
また、「
の倍数といえば、負のものや 0
も含みます。
また、「
![]() $3$ の倍数
$3$ の倍数![]() 」
というのは
」
というのは ![]() の倍数全体という意味です。
の倍数全体という意味です。