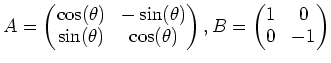Next: About this document ...
代数学 演習 C (コア) 問題 No.2
 群を取り扱うときには、群の定義 (0),(1),(2),(3) に戻って考えよう。
群を取り扱うときには、群の定義 (0),(1),(2),(3) に戻って考えよう。
- (i).
- 基本的には、普通の掛け算(あるいは、足し算)をやっていると思ってよい。
- (ii).
- 積は、可換とは限らない。
- (iii).
- 一般には、群の演算以外を用いてはならない。
問題 2.1
群
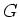
の元
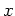
と、自然数
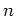
について、
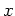
の
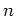
個の積
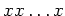
を
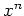
と書き、
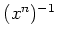
(
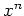
の逆元) を
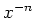
と書きます。
任意の整数
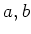
について、
が成り立つことを示しなさい。
問題 2.2
集合
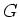
に演算
が定義され、この演算は結合法則を満たすとします。
さらに、
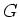
の任意の元
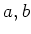
について、
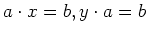
となる
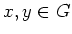
が存在したとします。
(一意性は仮定しない。)この時
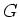
は群となることを示しなさい。
問題 2.3
群の元
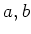
に対して、
が成り立つことを示しなさい。
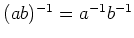
は
いつでも正しいといえますか?
(こういう問題では、正しい時には証明を、正しくない時には具体的な例を
あげることを要求しています。)
問題 2.4
有限個の元を持つ群
について、そのどの元
についても、
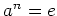
(
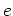
は単位元)となる自然数
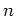
が存在する事を示しなさい。
問題 2.5
群
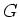
の任意の元
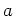
が、、
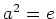
(
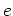
は
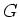
の単位元)
となるとすると、
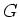
は実は可換群であることを示しなさい。
問題 2.6
一般に、群の元
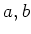
について、
は正しいといえますか?
問題 2.7
群
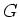
の元
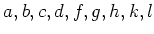
について、次の元をできるだけ簡単に表しなさい。
問題 2.8
群
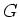
の二つの元
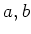
が、関係
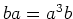
を満たすとき、
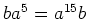
が成り立
つことを示しなさい。
問題 2.9
群
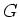
の二つの元
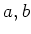
が次のような関係式を満た
すとします。
このとき、
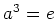
であることを示しなさい。
問題 2.10
群
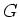
の元
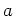
が
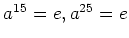
をみたすとき、
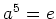
であることを示しなさい。
問題 2.11
群
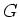
の二つの元
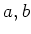
が次のような関係式を満た
すとします。
このとき、
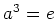
であることを示しなさい。
問題 2.12
群
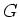
の二つの元
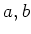
が次のような関係式を満た
すとします。
このとき、
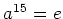
であることを示しなさい。
問題 2.14 (複素数の問題)
一般に、複素数
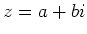
に対して、平面上の点
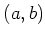
を対応させることができます。このとき、二つの複素数
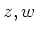
と、
- 和
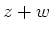
- 積
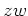
との位置関係が幾何学的にどうなっているかを述べなさい。
(ヒント:(1)平行四辺形の法則。(2)
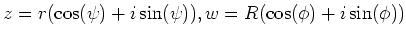 とおいてみなさい。(極座標表示))
とおいてみなさい。(極座標表示))
問題 2.15 (線型代数の復習)
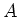
を 複素係数の
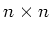
-行列とします。このとき、
(
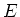
は単位行列)
となる自然数 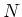 と、複素数
と、複素数
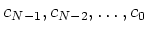 が存在することを示しなさい。
(ヒント、
が存在することを示しなさい。
(ヒント、
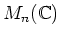 が有限次元であることに注意しなさい。)
が有限次元であることに注意しなさい。)
問題 2.16
実数
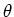
を一つ固定する。
二次正方行列
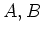
を、
で定める。このとき、
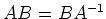
が成り立つことを示し、
さらにそれを用いて
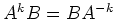
が成り立つことを示せ。



Next: About this document ...
2006-04-18
![]() 群を取り扱うときには、群の定義 (0),(1),(2),(3) に戻って考えよう。
群を取り扱うときには、群の定義 (0),(1),(2),(3) に戻って考えよう。
![]() とおいてみなさい。(極座標表示))
とおいてみなさい。(極座標表示))
![]() と、複素数
と、複素数
![]() が存在することを示しなさい。
(ヒント、
が存在することを示しなさい。
(ヒント、
![]() が有限次元であることに注意しなさい。)
が有限次元であることに注意しなさい。)