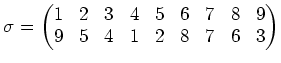1=6 1 by -1     

代数学 C 演習問題 No.6

定義 6.1   集合 $S$ の上に同値関係(同値律)が与えられているとは、 次のような条件を満たす 「$\equiv$ 」が 与えられている時にいいます。

1. $\equiv$ は $S$ の上の二項関係である。すなわち、$S$ の二つの元 $a,b$ に対して、 $a \equiv b$ かそうでないかがはっきり定まっている。
2. $a\equiv a \quad (\forall a\in S)$
3. $a\equiv b, b\equiv c \implies a\equiv c(\forall a,b,c \in S)$
4. $a\equiv b \implies b\equiv a(\forall a, b\in S)$

問題 6.1   次で定義される $\equiv_?$ の 各々はそれぞれ ${\mbox{${\mathbb{Z}}$}}$ 上の同値関係になっているかどうか、 理由をつけて答えなさい。

1. $x\equiv_1 y {\Leftrightarrow} x=y$
2. $x\equiv_2 y {\Leftrightarrow} x \leq y$
3. $x\equiv_3 y {\Leftrightarrow} ($$x-y$ は奇数$)$
4. $x\equiv_4 y {\Leftrightarrow} ($$x-y$ は偶数$)$
5. $x\equiv_5 y {\Leftrightarrow} x^2-y^2 \in 5{\mbox{${\mathbb{Z}}$}}$
6. $x\equiv_6 y {\Leftrightarrow} x-y\neq 0$
7. $x\equiv_7 y {\Leftrightarrow} ($$x=y$ かつ $x&ne#neq;0$$)$

問題 6.2  

1. 集合 $N=\{$日本人$\}$ において、 「誕生日が同じ」というのは同値関係であることを示しなさい。
2. 0 でない自然数 $k$ を一つ固定します。 (例えば $k=5$ としてもよろしい。) 整数全体の集合 ${\mbox{${\mathbb{Z}}$}}$ において、
   $$n\equiv m {\Leftrightarrow}n-m$$   は $k$ で割り切れる。
   できまる関係 $\equiv$ は同値関係であることを示しなさい。

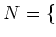
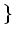
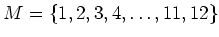
問題 6.3   前問との関連問題です。 $N=\{$日本人$\}$ から $M=\{1,2,3,4,\dots,11,12\}$ への「うまれ月写像」を、

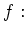
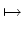
$$f:$$ある人$$\mapsto$$   その人のうまれ月

で定義します。

1. 次の 1から3は (あ) から(う)のどれに対応しているか答えなさい。

   1. 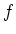$f$ はうまく定義されている。

   2. 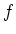$f$ は全射である。

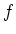   3. $f$ は単射ではない。

   (あ) 日本人の中には同じ生まれ月の人がいる。

   (い) 一人の人の生まれ月と言うのは一つしかない。

   (う) どの月をとってもだれか一人はその月の生まれがいる。

2. 生まれ月が同じというのは同値関係であることを示しなさい。

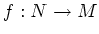
問題 6.4   一般の写像 $f:N\to M$ に対して、

$$n_1\equiv n_2 {\Leftrightarrow}f(n_1)=f(n_2)$$

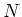
は $N$ における同値関係を与えることを示しなさい。 前問の (2) はこの問題の特殊な場合であることを示しなさい。

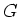
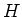
問題 6.5   群 $G$ の部分群 $H$ が与えられたとき、

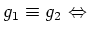
$$g_1 \equiv g_2 {\Leftrightarrow}$$ $g_1h=g_2$ となる $h&isin#in;H$が存在する。

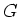
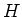
によって、$G$ における同値関係が定義されることを示しなさい。 $H$ が群であるための条件と同値関係の条件がどう対応しているかも確かめなさい。

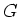
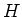
問題 6.6   群 $G$ の部分群 $H$ が与えられたとき、

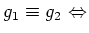
$$g_1 \equiv g_2 {\Leftrightarrow}$$ $hg_1=g_2$ となる $h&isin#in;H$が存在する。

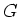
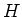
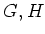
によって、$G$ における同値関係が定義されることを示しなさい。 $H$ が群であるための条件と同値関係の条件がどう対応しているかも確かめなさい。 さらに、この同値関係が前問の同値関係と本当に異なるような $G,H$ の例を 一つ与えなさい。

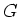
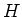
問題 6.7   群 $G$ の部分群 $H$ が与えられたとき、

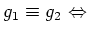
$$g_1 \equiv g_2 {\Leftrightarrow}$$ $hg_1=g_2h$ となる $h&isin#in;H$が存在する。

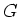
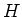
によって、$G$ における同値関係が定義されることを示しなさい。 $H$ が群であるための条件と同値関係の条件がどう対応しているかも確かめなさい。

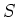
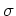
問題 6.8   集合 $S$ の上の置換 $\sigma$ が一つ与えられたとき、

$$s_1 \equiv s_2 {\Leftrightarrow}\exists k\in {\mbox{${\mathbb{Z}}$}};\quad \sigma^k(s_1)=s_2$$

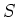
は $S$ における同値関係を定義することを示しなさい。

問題 6.9   前問で、 $S=\{1,2,3,4,5,6,7,8,9\}$ ,

$$\sigma= \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ 9 & 5 & 4 & 1 & 2 & 8 & 7 & 6 & 3 \end{pmatrix}$$

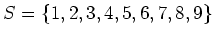
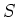
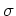
のとき、$S$ を $\sigma$ による前問の同値関係で クラスわけしなさい。

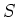
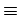
問題 6.10   同値関係の定義 6.1のうち、 1,3,4 は満たすけれども 2 は満たさないような $S$ と $\equiv$ の例を一つ挙げなさい。