代数学 C(コア) 演習問題 No.8

群の部分群による剰余集合が、「自然なやり方で」群になるには、その部分群が正規部分 群であればよろしい。

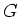
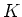
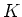
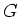
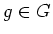
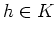
定義 8.1   $G$ を群、$K$ をその部分群とする。$K$ が $G$ の正規部分群であるとは、 任意の $g\in G$ と任意の $h\in K$ とに対して、

$$ghg^{-1}\in K$$

が成り立つときに言います。

問題 8.1   次の各組 $(G,S)$ について、$S$ は $G$ の部分群であるか、 理由をつけて答えなさい。

1. $G={\mbox{${\mathbb{Z}}$}}, S= \{0,1,2,\dots,\}$ .
2. $G={\mbox{${\mathbb{Z}}$}}, S=k{\mbox{${\mathbb{Z}}$}}\quad (k = 0,1,2, \dots)$ .
3. $G={\mbox{${\mathbb{Z}}$}}, S=\mbox{${\mathbb{R}}$}$ .
4. $G={\operatorname{GL}}_n($$\mbox{${\mathbb{R}}$}$$), S=\operatorname{SL}_n($$\mbox{${\mathbb{R}}$}$$)$ . 但し、

   $${\operatorname{GL}}_n( \mbox{${\mathbb{R}}$} )=\{A; \ A n \operatorname{det}(A)\neq 0 \},$$

   $$\operatorname{SL}_n( \mbox{${\mathbb{R}}$} )=\{A; A\in {\operatorname{GL}}_n( \mbox{${\mathbb{R}}$} ), \operatorname{det}A=1\}.$$

   
   
   (行列式の諸性質は自由に用いてよい。)

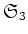
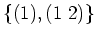
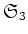
問題 8.2   3次の対称群 $\frak S_3$ の部分集合 $\{(1),(1\ 2)\}$ は $\frak S_3$ の 部分群ではあるが、正規部分群ではないことを示しなさい。

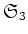
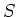
問題 8.3   $\frak S_3$ の部分集合 $S$ で、条件

$$gSg^{-1}=S \quad (\forall g \in \frak S_3)$$

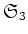
は満たすけれども $\frak S_3$ の正規部分群ではないものの例を 一つ挙げなさい。

問題 8.4   4次の対称群 $\frak S_4$ の正規部分群 $N$ が $(1\ 2)$ を元として含めば、

1. $N$ は $(2 \ 3),\ (3 \ 4)$ も元として含むことを示しなさい。
2. $N$ は $\frak S_4$ 全体に一致しなければならないことを示しなさい。

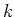
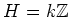
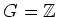
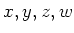
問題 8.5   正の整数 $k$ を一つ固定して、 $H=k{\mbox{${\mathbb{Z}}$}}$ とおきます。 $G={\mbox{${\mathbb{Z}}$}}$ の元 $x,y,z,w$ が、

$$x\equiv y ({\operatorname{mod}}\ H ), z\equiv w ({\operatorname{mod}}\ H)$$

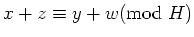
を満たすとすると、 $x+z \equiv y+w ({\operatorname{mod}}\ H)$ と言えるかどうか？理由を述べて答えなさい。

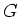
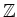
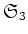
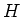
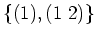
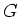
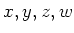
問題 8.6   前問で、$G$ として ${\mbox{${\mathbb{Z}}$}}$ のかわりに $\frak S_3$ をとり、$H$ として $\{(1),(1\ 2)\}$ をとります。$G$ の元 $x,y,z,w$ が、

$$x\equiv y ({\operatorname{mod}}\ H ), z\equiv w ({\operatorname{mod}}\ H)$$

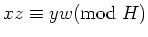
を満たすとすると、 $xz \equiv yw ({\operatorname{mod}}\ H)$ と言えるかどうか？理由を述べて答えなさい。

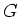
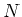
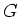
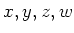
問題 8.7   $G$ は群であるとし、$N$ はその正規部分群であるとします。 $G$ の元 $x,y,z,w$ が、

$$x\equiv y ({\operatorname{mod}}\ N ), z\equiv w ({\operatorname{mod}}\ N)$$

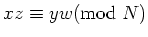
を満たすとすると、 $xz \equiv yw ({\operatorname{mod}}\ N)$ が成り立つことを示しなさい。

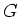
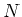
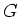
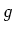
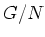
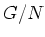
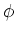
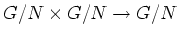
問題 8.8   $G$ は群であるとし、$N$ はその正規部分群であるとします。 $G$ の元 $g$ にたいし、その $G/N$ でのクラスを $[g]$ と書くことにします。 このとき、$G/N$ 上の演算 $\phi$ (つまり、写像 $G/N \times G/N \to G/N$ ) を、

$$\phi([x],[y])=[xy]$$

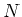
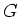
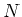
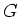
で定めることができることを示しなさい。(問題点はどこですか？ $N$ が $G$ の正規部分群ではなくて単なる部分群だとどこが困りますか？ $N$ が $G$ の部分群ですらない時にはどこが困りますか？)

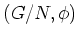
問題 8.9   前問で、 $(G/N, \phi)$ は群になることを示しなさい。

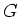
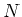
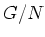
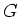
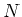
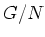
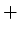
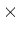
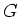
定義 8.2   前問のように、$G$ が群、$N$ がその正規部分群であれば、$G/N$ には 群の構造が入ります。この群のことを $G$ の $N$ による 剰余群といいます。 なお、$G/N$ の演算を表す記号 ($+$ or $\times$ ) は、 $G$ の演算を表す記号と同じものが 使われるのが普通です。

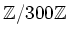
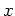
問題 8.10   ${\mbox{${\mathbb{Z}}$}}/300{\mbox{${\mathbb{Z}}$}}$ での足し算 $([175]+[200])+[50]$ を簡単な形に 直しなさい。また、 $[150]+[x]=[0]$ を満たす正の整数 $x$ の例を 一つ挙げなさい。

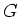
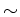
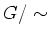
問題 8.11   $G$ を群とし、その上の同値関係 $\sim$ が定まっているとします。 $G/\sim$ に 乗法を、

$$% latex2html id marker 838\overline{a}\overline{b} = \over... ...(a,b\in G; \text{$\overline{a}$ 等は $a$ 等のクラスを表す。})$$

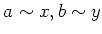
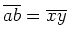
で定めようと思います。この乗法が代表元の取りかたによらずにうまく定義される (すなわち、 《 $a\sim x, b \sim y$ ならば いつでも $\overline{ab}=\overline{xy}$ が成り立つ》) ならば、

$$N=\{x\in G; \quad x \sim e\}$$

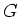
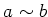
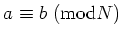
は $G$ の正規部分群となり、$a\sim b$ と $a\equiv b \ ({\operatorname{mod}}N)$ とは同値になる。 ということをしめしなさい。

問題 8.12   群 $G$ とその正規部分群 $N$ が与えられているとします。このとき、 次の二つは同値であることを示しなさい。

1. ある $n\in N$ があって、$xn=y$ と書ける。
2. ある $n\in N$ があって、$nx=y$ と書ける。

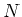
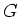
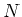
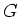
問題 8.13   前問で、「$N$ が $G$ の正規部分群である」と言う条件を 「$N$ が $G$ の部分群である」に置き換えると、1. と 2. とは 同値でなくなることを、実例を挙げて示しなさい。