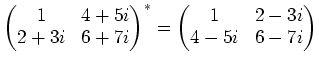問題 11.8
複素数を成分に持つ行列
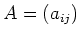
に対して、その随伴行列
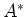
を、
で定義します。(すなわち、
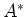
は、
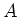
の転置行列
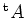
の各行列成分
についておのおのの複素共役をとったものです。) 例えば、
と言う具合です。この時、
- 複素数を成分に持つ
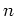 -次正方行列 (=
-次正方行列 (=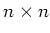 -行列)全体を
-行列)全体を
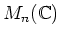 と書
けば、
と書
けば、
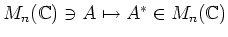 は行列の加法群
は行列の加法群
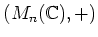 からそれ自体
への同型写像であることを示しなさい。
からそれ自体
への同型写像であることを示しなさい。
- 複素数を成分に持つ可逆
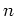 -次正方行列 (=
-次正方行列 (=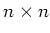 -行列)全体を
-行列)全体を
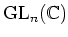 と書けば、
と書けば、
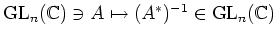 は可逆行列全体のなす乗法群
は可逆行列全体のなす乗法群
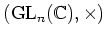 (一般線型群と呼ばれる)からそれ自体への同型写像であることを
示しなさい。
(一般線型群と呼ばれる)からそれ自体への同型写像であることを
示しなさい。
![]() 今回は、一学期の目標である《群の準同型定理》について
出題します。
今回は、一学期の目標である《群の準同型定理》について
出題します。