Next: About this document ...
1=3
代数学 C(コア) No.3要約
 《有限群》
《有限群》
 元の数が有限であるような群を、有限群と言う。
元の数が有限であるような群を、有限群と言う。
 群
群 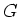 の元の個数を、
の元の個数を、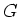 の位数と言い、
の位数と言い、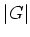 で表す。
で表す。
有限群の重要な例として、有限対称群、有限巡回群、二面体群がある。
定義 3.1
集合
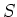
が与えられたとする。このとき
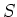
から
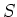
への全単射の全体は
写像の合成に関して群をなす。これを
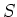
上の対称群と言う。
有限集合上の対称群を有限対称群と呼ぶ。
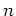
個の元からなる
集合
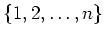
の上の対称群を、
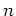
次の対称群と呼ぶ。
要は、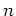 個の元
個の元 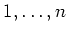 の置換全体のなす群が
の置換全体のなす群が 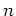 次の対称群である。
次の対称群である。
定理 3.1
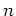 次の対称群の位数は
次の対称群の位数は 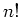 である。
である。
定義 3.2 (有限巡回群の定義)
元の数が有限である巡回群を、有限巡回群と言う。
定義 3.3
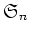
の元
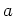
を
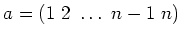
で定義する。
このとき、
を位数
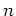
の有限巡回群と呼ぶ。
注意
上の元 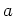 について、
について、
と書ける。だが、場合分けをするより、もっと楽な方法がある。
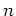 を決めておいて、
を決めておいて、
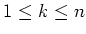 の範囲では、
の範囲では、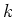 のかわりに
のかわりに
![$ [k]$](img17.png) という記号を導入する。
(どの
という記号を導入する。
(どの 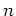 を考えているかはっきりさせたい時には
を考えているかはっきりさせたい時には ![$ [k]_n$](img18.png) と書くこともある。)
つぎに、一般の整数について、順繰りに、
と書くこともある。)
つぎに、一般の整数について、順繰りに、
等と約束する。
例えば、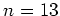 ならば、
ならば、
![$ [k]=[l]$](img25.png) かどうかは、
かどうかは、 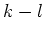 が
が 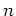 で割り切れるかどうかで
判断できることに注意しておこう。
で割り切れるかどうかで
判断できることに注意しておこう。
以上のようにしておいて、
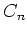 は
は
![$ \{[1],[2],[3],\dots,[n]\}$](img28.png) の置換だとみなすと、
の置換だとみなすと、
と書ける。これは以後の定理の証明に非常に有効である。
正 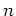 角形をそれ自身に重ねあわせる操作のなす群を二面体群と言う。
これをここでは次のように導入する。
角形をそれ自身に重ねあわせる操作のなす群を二面体群と言う。
これをここでは次のように導入する。
定義 3.4
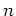
は
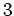
以上の整数であるとする。
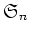 のなかで、
のなかで、
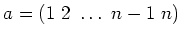 と、
と、
とで生成された群を
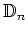
と書き、二面体群と言う。
注意
等式
が成り立つ。
さらに、 先ほど述べた ![$ [k]$](img17.png) という記号を用いると、
という記号を用いると、
が成り立つ。
※レポート問題
次の中から一問を選んで、レポートとして提出しなさい。
(期限:次の講義の終了時まで。)
- (I).
-
![$ a^k (b( a^l([x])))$](img43.png) および
および
![$ a^{k-l}(b([x])) $](img44.png) を計算することにより、
定理 5.3の 2.を証明しなさい。
を計算することにより、
定理 5.3の 2.を証明しなさい。
- (II).
-
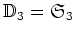 を示しなさい。
を示しなさい。



Next: About this document ...
2006-04-25
![]() 《有限群》
《有限群》
![]() 元の数が有限であるような群を、有限群と言う。
元の数が有限であるような群を、有限群と言う。
![]() 群
群 ![]() の元の個数を、
の元の個数を、![]() の位数と言い、
の位数と言い、![]() で表す。
で表す。
![]() について、
について、
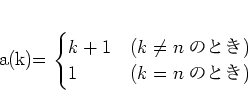
![]() は
は
![]() の置換だとみなすと、
の置換だとみなすと、
![]() のなかで、
のなかで、
![]() と、
と、