![]() 《同値関係》
《同値関係》
![]() 《同値関係》と《クラス分け》とは一つの現象を裏と表とから眺めたものである。
《同値関係》と《クラス分け》とは一つの現象を裏と表とから眺めたものである。
●定理3.3の証明の完結
定理3.3(再録)
の
注意: 次の例に垣間見られるように、一般に群の元が与えられた時にそれが生成する 部分群がどのようなものかを決定するのは上の例ほど単純ではない。
(例★)
![]() とし、
とし、
![]() とおく。
このとき,
とおく。
このとき,
![]() は
は
![]() や
や
![]()
![]() の形では表すことができない。
の形では表すことができない。
●定理2.5の証明
定理2.5(再録)
![]() の部分群は必ず
の部分群は必ず
のどれかである。(もちろん、
集合に同値関係を入れるということは、集合のクラス分けをする事と同じことになる。クラス分けの正確な定義は、次のようになる。
がなりたつ。
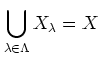
がなりたつ。(各
| (※) |
レポート問題
(I)
日常生活に現れる簡単な集合 ![]() とその上の同値関係
とその上の同値関係 ![]() の例をあげ、その例において
の例をあげ、その例において ![]() がどのようなものであるか
述べよ。
(条件の設定の仕方によっては同値関係と呼べるかどうか
怪しいものもある。そのようなものについては、どこが弱点か、
どのようにすれば改善するかも述べること。)
がどのようなものであるか
述べよ。
(条件の設定の仕方によっては同値関係と呼べるかどうか
怪しいものもある。そのようなものについては、どこが弱点か、
どのようにすれば改善するかも述べること。)
(II) (例★)の証明をつけよ。
(III)
(例★)において、
![]() で生成される
で生成される ![]() の部分群を求めよ。
の部分群を求めよ。