


Next: About this document ...
1=8
1 by -1
代数学 C No.8要約
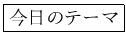
準同型とは、演算を保つ写像の事である。
定義 8.1
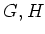
を群とする。
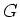
から
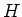
への写像
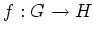
が準同型(正確には、群としての準同型写像)であるとは、
任意の
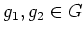
に対して、
が成り立つときに言う。 準同型
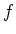
が全単射でもある時、
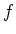
を同型と言う。
これまで、群には演算、というデータのほかに、単位元、逆元の存在が基本的である
と言ってきた。これらは準同型で自動的に保存される。次の定理でそのことを示そう。
 準同型の核
準同型の核
定義 8.2
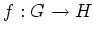
を二つの群の間の準同型とする。
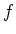
の核 (kernel) とは、
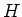
の単位元
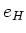
の
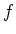
の逆像の事である。すなわち、
準同型を調べよ、と言われたらとりあえずその核を調べる。核は次のような性質と役割
をもつ。
定理 8.2
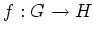 を二つの群の間の準同型とする。このとき、
を二つの群の間の準同型とする。このとき、
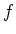 の核
の核
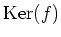 は
は 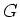 の正規部分群である。
の正規部分群である。
-
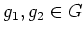 に対して、「
に対して、「
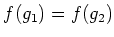 」 と 「
」 と 「
 」 とは同値である。
」 とは同値である。
上の定理はとても大事であるので、次回からも引き続き考えることになる。
(実力のある諸君はこの時点で準同型定理(NO.1 要約参照)
の証明を完結できる筈である。試していただきたい。)
※レポート問題
つぎのうち一問を選択して解きなさい。
(期限:次の講義の終了時まで。)
- (I).
- 例 8.2(1)において、「
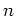 は
は 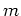 の倍数である」という条件を
取り去ると
の倍数である」という条件を
取り去ると 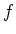 は群の準同型と言えるか、
は群の準同型と言えるか、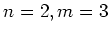 のときを例にとって
論じなさい。
のときを例にとって
論じなさい。
- (II).
- 二面体群
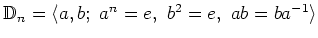 から
から
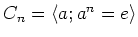 への写像
への写像 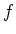 を、
を、
で定めると、これは (i)写像としてうまく定義されているけれども
(ii)群の準同型写像ではないという事を示しなさい。
- (III).
- 二面体群
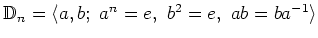 から
から
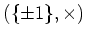 への写像
への写像 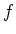 を、
を、
で定めると、これは群の準同型写像である事を示しなさい。



Next: About this document ...
2006-06-05
![]()
![]() 準同型の核
準同型の核