![]() 0=共役 1=きょうやく0>1 0=0 0=1
=0pt plus 2fil
=0pt plus 2fil
to 0きょうやく
to 0共役
0=共役 1=きょうやく0>1 0=0 0=1
=0pt plus 2fil
=0pt plus 2fil
to 0きょうやく
to 0共役
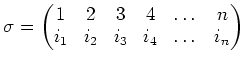
のとき、
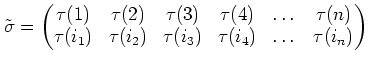
である。つまり、
なる関係式がもちろん成り立つ。この等式を類等式と呼ぶ。
なお、![]() の順番はどうでも良いと書いたが、通常 1番目は
の順番はどうでも良いと書いたが、通常 1番目は ![]() の単位元
の単位元 ![]() の
クラスに当てるのが普通である。この場合は
の
クラスに当てるのが普通である。この場合は ![]() になる。
になる。
つぎの命題の証明の考え方は、群の準同型定理に似たところがある。
で定義すると、
という等式が成り立つ。
※レポート問題