


Next: About this document ...
代数学 C No.13要約
今日のテーマ
定義 13.1
群
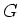
の集合
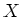
への作用とは、次のような条件を満たす写像
のことである。
-
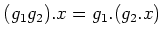 (
(
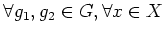 ).
).
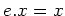 (
(
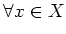 ).
).
例 13.1
群
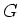
と、その部分群
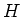
が与えられたとき、
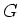
は
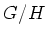
に
により作用する。(
![$ [x] $](img12.png)
は
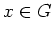
の
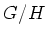
でのクラス).
例 13.2
群
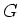
の
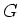
への作用を次の三種類定義することができる。
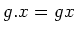 . (左作用)
. (左作用)
-
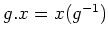 . (右作用)
. (右作用)
-
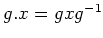 . (共役による作用).
. (共役による作用).
例 13.3
有限群
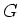
が与えられているとき、
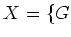
の部分群
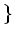
への
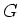
の作用が
により決められる。
更に、正の整数
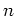
に対して、
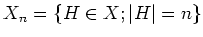
とおくと、
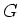
は
上記と同じ定義式により
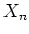
にも作用する。
補題 13.1
群 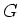 が有限集合
が有限集合 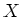 に作用しているとする。このとき
に作用しているとする。このとき 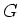 から
から
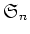 (
(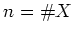 )への群準同型が定まる。
)への群準同型が定まる。
※レポート問題
問題 13.1
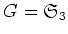
にたいし、
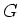
の部分群の全体
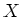
を考える。
このとき、
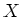 を求めよ。
を求めよ。
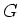 は共役により
は共役により 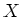 に作用するから、補題 13.1 のように
に作用するから、補題 13.1 のように
が定まる。この写像を具体的に書き下せ。
2006-07-10
![]()