In abstract algebra, we may find another way of describing the uncertainty principle. We first define the algebra generated by the operators appeared in the preceding subsection.
We call it the Weyl algebra over
In general, including the case where the characteristic of the ground field ![]() is non zero (or even the case where
is non zero (or even the case where ![]() is an arbitrary ring),
we define as follows.
is an arbitrary ring),
we define as follows.
Where
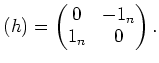
In what follows, ![]() will always mean the matrix above.
we denote by
will always mean the matrix above.
we denote by ![]() the inverse matrix of
the inverse matrix of ![]() .
.
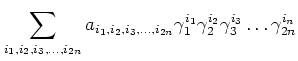
Then the fact is:
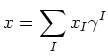
Then it is easy to see that the commutator
From the manner we choose the element ![]() , we deduce that
, we deduce that ![]() should be
a non zero constant in
should be
a non zero constant in
![]() . That means,
. That means,
This is contrary to the assumption that
![]()
When the characteristic of the base field ![]() is not zero,
things are different. We shall see this in the next section.
is not zero,
things are different. We shall see this in the next section.
Before that, we make an easy explanation for the latter part of the Lemma above. Let
be a finite dimensional representation. Then taking a trace of the CCR relations we obtain
which is absurd.