such that
such that
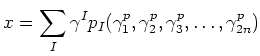
where sum is taken over multi-indices
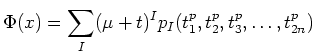
Now, let
This is contrary to the assumption that
The representation is ``universal". It contains all the information of
![]() and also carries all the irreducible finite-dimensional
representations as specializations.
and also carries all the irreducible finite-dimensional
representations as specializations.
Via this representation, any element of ![]() may be viewed as
a matrix-valued polynomial function
on the affine space
may be viewed as
a matrix-valued polynomial function
on the affine space
![]() .
.