DEFINITION 3.8
Let
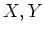
be topological spaces.
Let
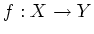
be a continuous map.
Let
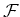
be a sheaf on
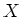
. Then we define its direct image
with respect to
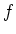
by
with obvious restriction maps.
EXAMPLE 3.11
Let
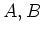
be rings. Let
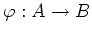
be a ring homomorphism.
We put
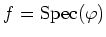
be the continuous map
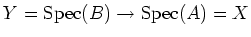
corresponding to
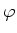
.
We note that
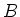
carries an
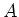
-module structure via
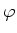
.
Accordingly, we have the corresponding sheaf
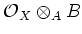
on
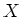
.
We may easily see that this sheaf coincides with
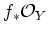
.
The map
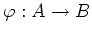
then may also be regarded as a homomorphism of
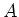
-modules.
We have thus an
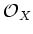
module homomorphism
of sheaves on
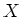
.
By the adjoint relation (Proposition
3.9),
we obtain a sheaf homomorphism
of sheaves of rings.
![]()
![]()