where
where
One may define localization in much more general situation. The reader is advised to read standard books on commutative algebras.
We need to show that it is injective, and that it gives a homeomorphism between
Let us do this by considering representations.
Now, for any
![]() ,
,
![]() extends to
extends to ![]() if and only if the image
if and only if the image
![]() of
of
![]() is invertible, that means,
is invertible, that means,
![]() .
In such a case, the extension is unique.
(We recall the fact that the inverse of an element of
a field is unique.)
.
In such a case, the extension is unique.
(We recall the fact that the inverse of an element of
a field is unique.)
It is easy to prove that
![]() is a homeomorphism.
is a homeomorphism.
![]()
Let ![]() be a ring. Let
be a ring. Let ![]() .
It is important to note that each element of
.
It is important to note that each element of ![]() is written as a
``fraction''
is written as a
``fraction''
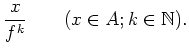
One may introduce
We introduce on
Then we may obtain a ring structure on
where we have denoted by
Likewise, for any ![]() -module
-module ![]() , we may define
, we may define ![]() as
a set of formal fractions
as
a set of formal fractions
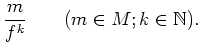
which satisfy certain computation rules.