

Next: curvature
Up: curvature of connections
Previous: curvature of connections
Let 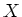 be a separated scheme over a scheme
be a separated scheme over a scheme 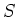 .
Let
.
Let
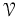 be a quasi coherent sheaf over
be a quasi coherent sheaf over 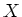 with a connection
with a connection
on it. We extend 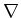 to
to
by defining
In other words,
It is easy to verify that 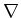 is well-defined and satisfy
is well-defined and satisfy
2007-12-26
![]() is well-defined and satisfy
is well-defined and satisfy