

Next: pairing of exterior algebras
Up: some linear algebra
Previous: some linear algebra
Before proceeding further, let us do a little definition and computation
on derivations.
DEFINITION 5.1
Let
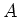
be a ring.
Let
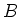
be a
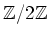
-graded A-algebra. Let
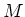
be a
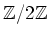
-graded
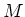
-module.
An
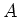
-linear map
is said to be
- an even derivation if it satisfies
and
holds.
- an odd derivation if it satisfies
and
holds.
Following [3], let us denote by
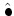 the
``parity'' of a homogeneous element
the
``parity'' of a homogeneous element 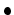 . That means,
. That means,
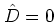 for an even derivation
for an even derivation 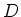 ,
and
,
and 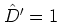 for an odd derivation
for an odd derivation 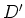 .
Then the ``Leibniz rules'' of the definition above may be
simply rewritten as
.
Then the ``Leibniz rules'' of the definition above may be
simply rewritten as
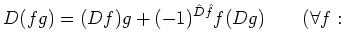
homogeneous
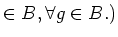
For convenience, let us call a map 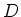 a graded derivation
if it is either an even derivation or an odd derivation.
a graded derivation
if it is either an even derivation or an odd derivation.
DEFINITION 5.2
Let
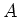
be a ring. Let
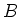
be a
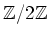
-graded
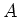
-algebra
Let
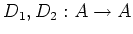
be graded derivations.
Then we define their
Lie bracket by
Caution:
The bracket defined here differs from the ordinary ``commutator''
if (and only if) both 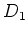 and
and 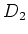 are odd. In such a case
it would be better to write
are odd. In such a case
it would be better to write
![$ [D_1,D_2]_+ $](img137.png) instead to avoid confusion.
instead to avoid confusion.
PROPOSITION 5.3
In the assumption of the definition above, the Lie bracket
![$ [D_1, D_2]$](img138.png) is an even or odd derivation with the parity
is an even or odd derivation with the parity
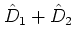 .
.
PROOF..
We first compute
Then by adding this equation with the one with
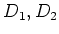
interchanged,
we obtain the required result.
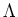
The following easy lemma is frequently used.
LEMMA 5.4
Let 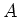 be a ring. Let
be a ring. Let 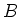 be a
be a
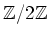 -graded algebra.
Let
-graded algebra.
Let 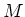 be a
be a
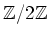 -graded
-graded 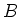 -module.
Then for any graded
-module.
Then for any graded 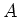 -derivation
-derivation 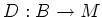 ,
The kernel of
,
The kernel of 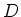 forms an
forms an 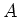 -subalgebra of
-subalgebra of 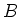 .
.
ARRAY(0x91ed2b4)


Next: pairing of exterior algebras
Up: some linear algebra
Previous: some linear algebra
2007-12-26
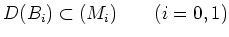
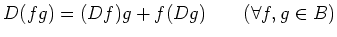
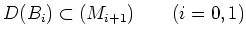
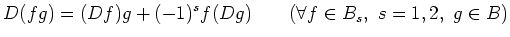
![]() the
``parity'' of a homogeneous element
the
``parity'' of a homogeneous element ![]() . That means,
. That means,
![]() a graded derivation
if it is either an even derivation or an odd derivation.
a graded derivation
if it is either an even derivation or an odd derivation.
![]() and
and ![]() are odd. In such a case
it would be better to write
are odd. In such a case
it would be better to write
![]() instead to avoid confusion.
instead to avoid confusion.
![]()