

Next: functoriality
Up: connection
Previous: definition of connections on
The first definition in the previous subsection is important because
one may easily recognize that the following type of lemma should hold.
LEMMA 1.1
Let 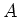 be a commutative ring. Let
be a commutative ring. Let 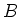 be a commutative
be a commutative 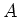 -algebra.
Let
-algebra.
Let 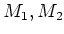 be
be 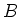 -modules with connections
-modules with connections
Then we may define a connection on the direct sum
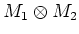 ,
on the tensor product
,
on the tensor product
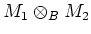 , and on the module
, and on the module
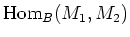 .
Namely,
.
Namely,
PROOF..
Easy.
2007-12-26
![]()