Let us define operators(matrices)
![]() acting on
acting on
![]() -dimensional vector space
-dimensional vector space
by
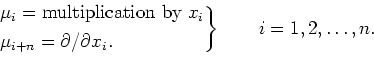
Let
be a polynomial ring of
Then we have a faithful representation
of the Weyl algebra
Furthermore, for any
by putting
We recall also that
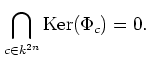
Here is another thing we need to know.
For any
So the image
Now, both
![]() and
and
![]() is free
is free ![]() -modules
of rank
-modules
of rank ![]() . So the map
. So the map
![]() is generically injective.
(That means,
if we take the quotient field
is generically injective.
(That means,
if we take the quotient field ![]() of
of ![]() and consider
and consider
then by an elementary theorem in linear algebra, we see that it is an isomorphism.)
Since ![]() (a polynomial algebra over
(a polynomial algebra over ![]() is an integral domain,
is an integral domain,
![]() is
is ![]() -torsion free.
(That means,
-torsion free.
(That means,
is injective.)
So we see that
![]() is injective.
is injective.
![]()