We have the following obvious lemma.
PROOF..
(1)
Since
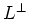
has a trivial Killing form, it is solvable.
(Cartan's criterion.)
Thus, by the maximality of
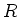
, we have
On the other hand, let us take an arbitrary
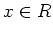
, then
for any
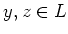
, we have
![$\displaystyle (\operatorname{ad}(x)\operatorname{ad}(y))^2 z\in [x,[y,R]]\subset [x,R]=0 \quad
($](img655.png)
Since $R$ is abelian.
So
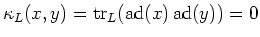
(as a trace of a nilpotent element.)
Thus
also holds.
(2):follows from the general theory.
(3):follows easily from the definition of  .
.
(4):Let us take an arbitrary  .
For any
.
For any 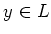 , we have by using(2)
, we have by using(2)
Thus
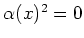
.
(5): follows clearly from (3).
(6): follows from (4),(5) and Engel's theorem.
(We need to note that
holds.)
(7):
The action of
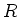
on
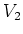
is equal to zero. So
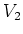
admits an action by
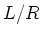
, which is semisimple. Now consider the following exact sequence of
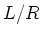
-modules.
where
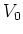
is the kernel of the restriction map.
By a special case of Weyl's theorem on complete reducibility
(Lemma
5.51),
We see that the sequence splits. (Since we assumed
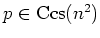
).
This implies that there exists an element
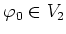
such that
Thus
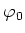
gives a splitting of the injection
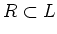
.
A Levi subalgebra of
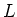
is obtained by putting
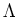
PROOF..
If
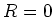
, then we only need to set
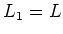
. So let us assume
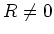
.
Let us put
Then from the definition, we
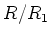
is an abelian Lie algebra.
It is also easy to verify that
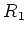
is an ideal of
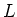
.
(
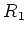
is a
characteristic ideal of
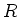
).
We apply the preceding lemma for
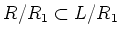
to obtain a Levi subalgebra
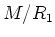
of
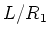
.
Then
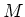
satisfies the following relations.
Since
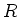
is solvable (and we have assumed
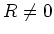
), we see that
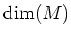
is strictly smaller than
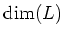
. By induction
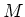
have a Levi subalgebra
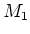
. Then it is clear that
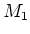
is a
Levi subalgebra of
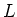
.
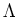
![]() .
.
![]() .
For any
.
For any ![]() , we have by using(2)
, we have by using(2)
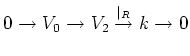
![]()