


Next: About this document ...
代数学III 要約 No.3
今日のテーマ

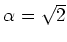 のとき、
のとき、
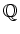
![$ [\alpha]$](img4.png) の元は
の元は 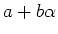
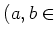
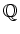
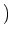 と書くことができ、それらの和、差、積、商の公式は
と書くことができ、それらの和、差、積、商の公式は
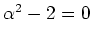 という関係式だけから書き下すことができるのであった。
もっと一般に、代数方程式を満たす元を体に「付け加える」ことができる。
(補題 3.1,定理 3.1)それには、多項式環をうまく用いる。
という関係式だけから書き下すことができるのであった。
もっと一般に、代数方程式を満たす元を体に「付け加える」ことができる。
(補題 3.1,定理 3.1)それには、多項式環をうまく用いる。
定義 3.1
体
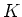
の元を係数に持つような
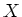
を変数とする一変数多項式の
全体を
![$ K[X]$](img11.png)
と書き、
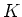
上の(
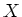
を変数とする)一変数多項式環と呼ぶ。
ついでに環とイデアルの定義を思い出しておこう。詳しくは代数 Iの講義を
復習すること。
定義 3.3
体
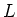
とその部分体
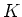
が与えられているとする。
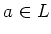
に対して、
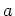
が満足する
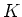
上の方程式、すなわち
をみたすもの
のうち次数が最小のものを、
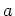
の
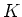
上の最小多項式と呼ぶ。
以下では、とくに断らない限り最小多項式と言えばモニックのものを指すことにする。
つぎの定理は、「方程式の解を付け加えること」が
形式的にはどのようなことを意味するかを説明する。
問題 3.1
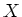
の4次式
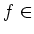
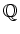
![$ [X]$](img37.png)
で、
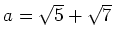
にたいして
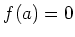
を
満たすようなものを見つけなさい。
問題 3.2
前問の
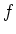
は
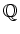
上既約であることを示しなさい。
(前問と本問をあわせると、
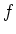
が
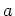
の最小多項式であることが
わかる。ただし今の段階ではかなり難しい問題である。
この講義のもっとあとの段階まで進めば、この問題も非常に易しく解けるようになる。)



Next: About this document ...
2006-10-23
![]()
![]() のとき、
のとき、
![]()
![]() の元は
の元は ![]()
![]()
![]()
![]() と書くことができ、それらの和、差、積、商の公式は
と書くことができ、それらの和、差、積、商の公式は
![]() という関係式だけから書き下すことができるのであった。
もっと一般に、代数方程式を満たす元を体に「付け加える」ことができる。
(補題 3.1,定理 3.1)それには、多項式環をうまく用いる。
という関係式だけから書き下すことができるのであった。
もっと一般に、代数方程式を満たす元を体に「付け加える」ことができる。
(補題 3.1,定理 3.1)それには、多項式環をうまく用いる。