


Next: About this document ...
代数学III 要約 No.7
今日のテーマ

定義 7.1
体
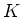
の有限次代数拡大体とは、
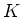
の拡大体で、
拡大次数が有限のものをいう。
前回の講義で、次の二つのことを用いた。(証明済み)
定理 7.1
体 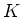 上の一変数多項式
上の一変数多項式
![$ f(X)\in K[X]$](img3.png) が与えられたとき、
が与えられたとき、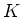 上の
有限次代数拡大体
上の
有限次代数拡大体 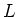 で、
で、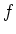 は
は 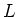 上一次式の積に分解するようなものが存在する。
上一次式の積に分解するようなものが存在する。
命題 7.2
体 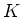 は有理数体
は有理数体
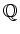 を含むとする。 このとき、
を含むとする。 このとき、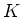 上代数的な元
上代数的な元 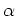 の
の 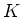 上の最小多項式は重根を持たない。
上の最小多項式は重根を持たない。
今回は次回以降の準備のためにつぎの定理を証明する。
定理 7.3
任意の対称式は基本対称式であらわせる。
詳しく言うと、
-
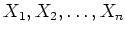 の多項式で、対称式になっているものは
基本対称式の多項式として書き表すことができる。
の多項式で、対称式になっているものは
基本対称式の多項式として書き表すことができる。
-
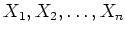 の有理式で、対称式になっているものは
基本対称式の有理式として書き表すことができる。
の有理式で、対称式になっているものは
基本対称式の有理式として書き表すことができる。
上の定理から次の系が直ちに従う。
系 7.1
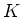 上の一変数
上の一変数 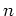 次多項式
次多項式 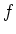 の根を
の根を
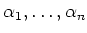 とする。
とする。
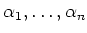 の対称式で書けるような元は全て
の対称式で書けるような元は全て 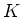 の元である。
の元である。
定理の証明には、次の記号を用いるのが便利である。(ただし、一般に
通用する記号というわけではない。)
記号
単項式
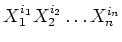 のうち、変数の入れ換えに
よって生じるものを全て(重複を除いて)集めて足したものを、ここでは、
のうち、変数の入れ換えに
よって生じるものを全て(重複を除いて)集めて足したものを、ここでは、
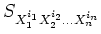 とかく。 たとえば、3変数なら、
とかく。 たとえば、3変数なら、
等等である。(ただし、
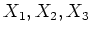 と書くと煩わしいので
と書くと煩わしいので 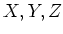 と書いた。)
と書いた。)
この記号を使えば、
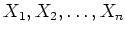 の基本対称式は、
の基本対称式は、
と書き表すことができる。
問題 7.1
三変数 (
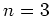
) のとき、
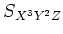
を 基本対称式の多項式で表しなさい。
2006-11-17
![]()
![]() のうち、変数の入れ換えに
よって生じるものを全て(重複を除いて)集めて足したものを、ここでは、
のうち、変数の入れ換えに
よって生じるものを全て(重複を除いて)集めて足したものを、ここでは、
![]() とかく。 たとえば、3変数なら、
とかく。 たとえば、3変数なら、
![]() の基本対称式は、
の基本対称式は、