


Next: About this document ...
代数学III 要約 No.11
今日のテーマ

定義 11.1
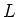
が
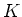
のガロア拡大のとき、
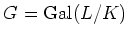
の部分群
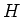
に対して、
とおく。
これは
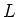
と
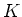
の中間体である。
つぎのことはすぐにわかる。
補題 11.1
上の定義の仮定のもとで、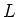 は
は 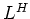 のガロア拡大である。
さらに、
のガロア拡大である。
さらに、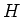 は自然に
は自然に
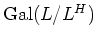 の部分群とみなせる。
の部分群とみなせる。
今日示したい重要な事実は、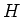 が実は
が実は
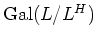 と一致することである。
(下の定理 11.1.)
そのためにつぎの補題を用いる。証明には「
と一致することである。
(下の定理 11.1.)
そのためにつぎの補題を用いる。証明には「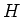 による対称化(平均化)」の
テクニックを用いる。
による対称化(平均化)」の
テクニックを用いる。
補題 11.2
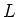 は
は 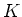 のガロア拡大であるとする。
任意の
のガロア拡大であるとする。
任意の 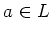 と
と
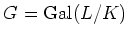 の部分群
の部分群 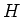 に対して、
に対して、
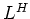 -係数のモニックな多項式
-係数のモニックな多項式 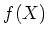 で、次の性質を満たすものが存在する。
で、次の性質を満たすものが存在する。
-
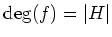
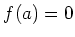
系 11.1
上の補題の仮定のもとで、
![% latex2html id marker 798
$ [L:L^H]\leq \vert H\vert$](img13.png) .
.
この系から直ちに、求めたかったつぎのことがわかる。
2006-12-14
![]()
![]() が実は
が実は
![]() と一致することである。
(下の定理 11.1.)
そのためにつぎの補題を用いる。証明には「
と一致することである。
(下の定理 11.1.)
そのためにつぎの補題を用いる。証明には「![]() による対称化(平均化)」の
テクニックを用いる。
による対称化(平均化)」の
テクニックを用いる。