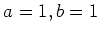 のとき、
のとき、
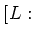
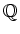
![$ ]$](img11.png) を求めよ。
を求めよ。
-
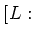
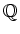
![$ ]=2$](img12.png) なる
なる 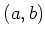 を2組求め、そのときの
を2組求め、そのときの 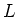 を
それぞれ求めよ。
を
それぞれ求めよ。
解答:
(1)
![]()
![]()
![]() とおく。
とおく。
![]() であって、なおかつ
であって、なおかつ
![]()
![]()
![]() であることを示そう。
そうすれば
であることを示そう。
そうすれば
であることがわかる。
Part 0)まずつぎの補題を証明しておく。
ならば
と書ける。両辺を二乗すると
仮定により、
とくに 後者の式から
(i) ![]() の場合。
の場合。
すなわち
がなりたつ。これは
(ii) ![]() の場合。
の場合。
がなりたつ。これは
どの場合も矛盾が生じたから、補題が正しいことが証明されたことになる。
![]()
Part I)
![]()
![]()
![]() を求めよう。それには
を求めよう。それには
なる部分体の列を考えて、各ステップでの拡大次数を各々求めれば良い。 それぞれのステップでは、平方根を一つだけ付け加えているのであるから、 拡大次数は2か、または 1(全く拡大していない)かのいずれかである。
講義で述べたように、![]() は有理数でない。したがって、
は有理数でない。したがって、
つぎに、
![]() のいずれも
のいずれも
![]() の元でないことから、補題を用いて、
の元でないことから、補題を用いて、
![]()
![]() がわかる。ゆえに、
がわかる。ゆえに、
さらに、
![]()
![]()
![]() である。これを
示そう。背理法で、
である。これを
示そう。背理法で、
![]()
![]()
![]() と仮定すると、補題を
と仮定すると、補題を
![]()
![]()
![]() の場合にもちいて、
の場合にもちいて、
![]() の
いずれかが
の
いずれかが
![]()
![]() に属さねばならなくなる。再び補題を
(今度は
に属さねばならなくなる。再び補題を
(今度は
![]()
![]() として)もちいると、
として)もちいると、
のいずれかが
よって、
結局
![]()
![]() は
は
![]() 上のベクトル空間として
上のベクトル空間として
の
Part II)
![]()
![]()
![]() を求めよう。
を求めよう。
![]() の
の
![]() 上の生成元
上の生成元
![]() の
共役はそれぞれ
の
共役はそれぞれ ![]() のなかに存在するので、
のなかに存在するので、![]() は
は
![]() の
有限次正規代数拡大、すなわちガロア拡大である。
の
有限次正規代数拡大、すなわちガロア拡大である。
![]()
![]()
![]() の元は
の元は
![]() の
各々の行き先(それぞれ二通り)を決めてやると決まり、高々 8個しかない。
の
各々の行き先(それぞれ二通り)を決めてやると決まり、高々 8個しかない。
他方で、
![]()
![]()
![]()
![]()
![]() であるから、結局上記可能性の
すべてがガロア群の元として許されることになる。すなわち、
であるから、結局上記可能性の
すべてがガロア群の元として許されることになる。すなわち、
![]() にたいして、
にたいして、
![]()
![]()
![]() を
を
Part III) ![]() を示そう。
を示そう。
![]() を
を
![]() .
に作用させると、
.
に作用させると、
Part I) の最後に注意したように、
がわかる。とくに、
(2)
であるから、
である。
(あ)
![]() , すなわち
, すなわち
![]() のとき。
のとき。
このときは
![]()
![]()
![]()
![]() である。
である。
(い)
![]() , すなわち
, すなわち
![]() のとき。
のとき。
このときは
![]()
![]()
![]()
![]() である。
である。
(う)
![]() , すなわち
, すなわち
![]() のとき。
のとき。
このときは
![]()
![]()
![]()
![]() である。
である。