


Next: About this document ...
数学概論1A要約 No.4

お持ち帰りにいたしますか?ここでお食べになりますか?
-どちらでもいいです. (マクドナルドにて by フヘ)
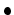 三角不等式
三角不等式
定理 4.1 (テキスト``定理1.2'')
-
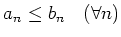 で、かつ
で、かつ 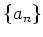 ,
, 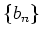 が
収束するなら、
が
収束するなら、
-
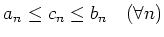 で、かつ
で、かつ 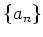 ,
, 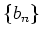 が
同じ数
が
同じ数 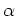 に収束するなら、
に収束するなら、 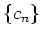 も
も 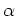 に収束する。
に収束する。
定理 4.2 (テキスト``定理1.3'')
収束する数列は有界である。
定理 4.3 (テキスト``定理1.4'')
実数列 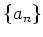 ,
, 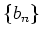 はそれぞれ収束するとする。このとき、
はそれぞれ収束するとする。このとき、
- 「極限をとる」という操作は線形である。すなわち、
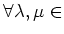
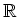 に対して
に対して
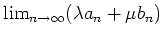 は収束して、
は収束して、
- 「実数の乗法は連続である。」
- 実数の除法は「連続」である。 もっと詳しく言うと、
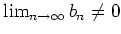 なら、
有限個の例外を除いて
なら、
有限個の例外を除いて 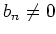 であって、
であって、
定義 4.1
実数列
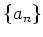
が単調増加であるとは、
がなりたつときにいう。
次の定理は、既知の数から未知の数 (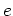 など) を作り出すときに有効である。
など) を作り出すときに有効である。
定理 4.4 (テキスト``定理1.5'')
上に有界な単調増加数列は収束する。
問題 4.1
実数列
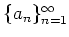
が
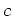
に収束するとき、
は収束すると言えるだろうか。言えるならばその収束先と理由を、言えないならば
反例を作りなさい。
2007-05-02
![]()
![]() 三角不等式
三角不等式
![]() など) を作り出すときに有効である。
など) を作り出すときに有効である。