をみたす
をみたす
(解答)
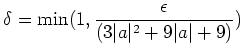
と置けば良い。 実際、このとき、
とすると
| (あ) | ||
| (い) |
| (う) |
をみたす
(解答)
とおけばよい。 実際、このとき、
とすると
| (あ) | ||
| (い) |
| (う) |
| (え) |
がなりたつ。これらに注意して
![]() を下のように評価すれば良い。
を下のように評価すれば良い。
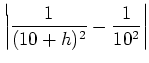 |
||
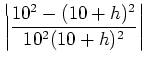 |
||
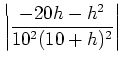 |
||
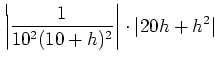 |
||
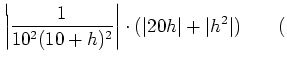 三角不等式 三角不等式 |
||
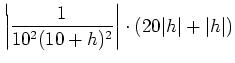 |
||
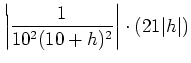 |
||
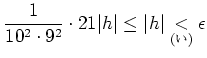 |
![]()
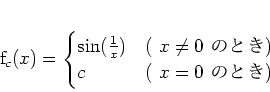
と定義する。この時、
(解答)
(1) (S1), (S2) により、
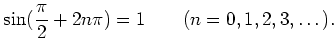
が容易にわかる。 よって、
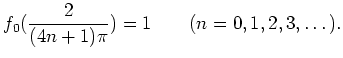
もし仮に ![]() が
が ![]() で連続であったとすると、
(連続性の定義の
で連続であったとすると、
(連続性の定義の ![]() として
として
![]() を採用して、)
を採用して、)
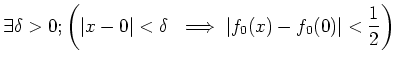 |
(あ) |
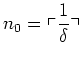
(すなわち、
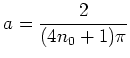
とおくと、
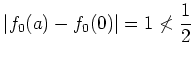
であることがわかる。 (この解答例では詳細は略するが、実際には確かめたほうが良い。) これは (あ) と矛盾するから、
(2) (S1), (S3) により、
が容易にわかる。 あとは、連続性の定義の
![]()
(解答の注意と補記)
(注意)
問題15.1 では、三角不等式の使い方が誤っている誤答例をよく見かけた。 ただしくなりたつのは
や
である。(なお、後者は前者の変数変換により容易に得られる。)
問題15.2 のポイントは、分母の評価である。 分母、分子ともに正の数の分数においては、 分母が小さくなるほど値が大きくなる。 したがって、解答例の(え)のような評価が必要である。
問題15.3 のグラフは教科書のP.18 にある。(ただし ![]() の部分だけ)
この関数の
の部分だけ)
この関数の ![]() での値をどう定めようと決して連続にはなり得ない
というのが問題の意味。解答例では
での値をどう定めようと決して連続にはなり得ない
というのが問題の意味。解答例では ![]() として
として
![]() を採用したが、もちろん他の値でも良い。ガウス記号を用いるのも良いし、
日本語で「○○より大きい整数」のように書いても良い。
を採用したが、もちろん他の値でも良い。ガウス記号を用いるのも良いし、
日本語で「○○より大きい整数」のように書いても良い。
(補記)
問題15.1, 15.2 は関数の連続性を問う問題である。
実際にはこれらの式の連続性を言うには、教科書の定理1.11 を
用いるほうがずっと易しい。
たとえば、問題15.1 の ![]() の連続性を確かめるにはつぎのようにしてやればよい。
の連続性を確かめるにはつぎのようにしてやればよい。