


: この文書について...
代数学 I No.7要約
 《環の準同型定理の利用法》
《環の準同型定理の利用法》
例 7.1 (準同型定理の基本例1)
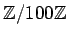
から
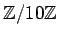
への写像

を、
![% latex2html id marker 1091
$\displaystyle f([n]_{100})=[n]_{10} \quad \quad ($](img5.png)
$[?]_n$ は $$
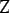
$/n$
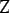
$$ における
$?$ の同値類
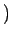
で定めると、次のことが分かる。
 は写像としてうまく定義されている。
すなわち、
は写像としてうまく定義されている。
すなわち、 の定義は代表元のとり方によらない。
の定義は代表元のとり方によらない。
 は環の準同型である。
は環の準同型である。
 の像は
の像は
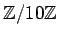 全体である。
全体である。
 の核は
の核は
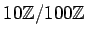 である。
である。
よって、準同型定理により、
が結論される。
例 7.2
環としての同型
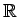
![$ [X]/(X^2+1)$](img11.png)
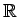
![$ [X] \cong {\mathbb{C}}$](img12.png)
が
存在する。
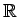
![$ [X]$](img13.png)
から
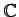
への写像

を、
で定めると、次のことが分かる。
 は写像としてうまく定義されている。
は写像としてうまく定義されている。
 は環の準同型である。
は環の準同型である。
 の像は
の像は
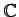 全体である。
全体である。
 の核は
の核は
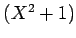
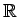
![$ [X]$](img13.png) である。
である。
よって、準同型定理により、
が結論される。
例 7.3 (準同型定理の応用例1)
![$ {\mbox{${\mathbb{Z}}$}}[X]$](img20.png)
から
![% latex2html id marker 1149
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{14}]$](img21.png)
への写像

を、
で定めると、次のことが分かる。
 は写像としてうまく定義されている。
すなわち、
は写像としてうまく定義されている。
すなわち、 の像は
の像は
![% latex2html id marker 1159
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{14}]$](img23.png) からはみ出さない。
からはみ出さない。
 は環の準同型である。
は環の準同型である。
 の像は
の像は
![% latex2html id marker 1165
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{14}]$](img24.png) 全体である。
全体である。
 の核は
の核は
![$ (X^2-14){\mbox{${\mathbb{Z}}$}}[X]$](img25.png) である。
である。
よって、準同型定理により、
が結論される。
例 7.4 (準同型定理の応用例2)
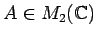
を、
で定め、
![$ {\mathbb{C}}[X]$](img29.png)
から
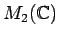
への写像

を、
で定めると、次のことが分かる。
 は環の準同型である。
は環の準同型である。
 の像は
である。
の像は
である。
 の核は
の核は
![$ (X^2-8 X-8){\mathbb{C}}[X]$](img33.png) である。
である。
よって、準同型定理により、
が結論される。
※レポート問題
つぎのうち一問を選択して解きなさい。
(期限:次の講義の終了時まで。)
- (I).
-
を
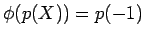 で定義すると、
これはうまく定義されていることを示しなさい。
で定義すると、
これはうまく定義されていることを示しなさい。
-
を
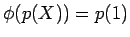 で定義しようとすると、
これはうまく定義されていないことを示しなさい。
で定義しようとすると、
これはうまく定義されていないことを示しなさい。
- (II).
-
を示しなさい。



: この文書について...
平成19年11月29日
![]() 《環の準同型定理の利用法》
《環の準同型定理の利用法》
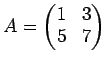
![$\displaystyle {\mathbb{C}}[A]=
{\mathbb{C}}A+{\mathbb{C}}E= \{k A+ lE ; k,l \in...
...in{pmatrix}
k+l &3k \\
5k &7k+l
\end{pmatrix}; k,l \in {\mathbb{C}}
\right \}
$](img32.png)