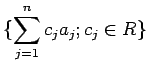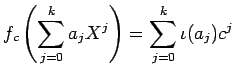: この文書について...
代数学 I No.9要約
 生成するイデアル, 多項式環の性質
生成するイデアル, 多項式環の性質
補題 9.1
可換環
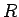
と、
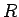
の部分集合
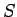
について、
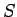
を含む
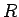
のイデアルのうち最小のものが存在する。
定義 9.1
可換環
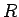
と、
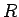
の部分集合
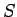
について、
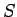
を含む
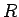
のイデアルのうち最小のものを、
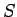 で生成される
で生成される
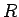 のイデアル
のイデアル といい、
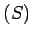
と表す。
丸括弧は、区切りを表す以外には
何の付加的な意味を持たないのが普通であるが、この用法は例外である。
補題 9.2
可換環
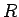
の有限部分集合
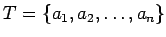
に対して、
が成り立つ。
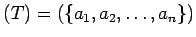
のことを普通
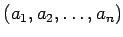
と書く。
(
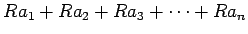 とは
とは
の略記であることに注意しよう。)
&dotfill#dotfill;
補題 9.3
-
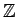 から環
から環 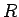 への準同型は必ず唯一つだけ存在する。
への準同型は必ず唯一つだけ存在する。
-
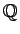 から環
から環 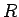 への準同型は、存在すれば唯一つである。
への準同型は、存在すれば唯一つである。
- 正の整数
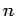 が与えられた時、
が与えられた時、
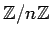 から環
から環 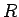 への環準同型は、
存在すれば唯一つである。
への環準同型は、
存在すれば唯一つである。
補題 9.4 (多項式環の普遍性)
可換環
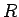
から
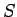
への環準同型
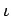
が与えられているとする。
このとき、
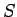 の元
の元 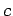 を与えると、
を与えると、
![$ R[X] $](img17.png) から
から 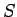 への環準同型
への環準同型 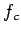 が、
すなわち、
で定まり、
が、
すなわち、
で定まり、
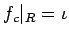 が成り立つ。
が成り立つ。
![$ R[X] $](img17.png) から
から 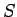 への環準同型
への環準同型 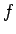 で、
で、
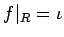 をみたすものが
あれば、ある
をみたすものが
あれば、ある 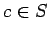 が存在して、
が成り立つ。
が存在して、
が成り立つ。
※レポート問題
つぎのうち一問を選択して解きなさい。
(期限:次の講義の終了時まで。)
- (I).
-
![$ ({\mbox{${\mathbb{Z}}$}}/10{\mbox{${\mathbb{Z}}$}})[X]$](img26.png) から
から
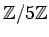 への環準同型は何個有るか。
への環準同型は何個有るか。
-
![$ ({\mbox{${\mathbb{Z}}$}}/9{\mbox{${\mathbb{Z}}$}})[X]$](img28.png) から
から
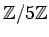 への環準同型は何個有るか。
への環準同型は何個有るか。
平成19年11月29日
![]() 生成するイデアル, 多項式環の性質
生成するイデアル, 多項式環の性質
![]() とは
とは