$\mathbb{Z}_p$ , $\mathbb{Q}_p$ , and the ring of Witt vectors

No.09:

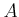
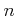
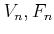
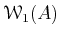
DEFINITION 09.1   Let $A$ be any commutative ring. Let $n$ be a positive integer. Let us define additive operators $V_n,F_n$ on $\mathcal W_1(A)$ by the following formula.

$$V_n(f(T))=f(T^n).$$

$$F_n(f(T))=\prod_{\zeta\in \mu_n} f(\zeta T^{1/n})$$

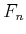
(The latter definition is a formal one. That means, $F_n$ is actually defined to be the unique continuous additive map which satisfies

$$F_n(1-a T^l)= (1-a ^{m/l} T^{m/n})^{l n/m} \qquad(m=l.c.m(n,l)).$$

)

LEMMA 09.2   Let $p$ be a prime number. Let $A$ be acommutative ring of characteristic $p$ . Then:

1. We have
   $$F_p(f(T))=(f(T^{1/p}))^{p} \qquad (\forall f\in \mathcal W_1(A)).$$
   in partucular, $F_p$ is an algebra endomorphism of $\mathcal W_1(A)$ in this case.

2. $$V_p(F_p(f)=F_p (V_p(f))=(f(T))^p=p \boxdot f(T) (=\overbrace{f(T)\boxplus\dots \boxplus f(T)}^{p}).$$

DEFINITION 09.3   Let $A$ be any commutative ring. Let $p$ be a prime number. We denote by

$$\mathcal W^{(p)} (A)=A^{\mathbb{N}}.$$

and define

$$\pi_p: \mathcal W_1(A) \to \mathcal W^{(p)}(A)$$

by

$$\pi_p \left ( \sideset{}{^{\boxplus }}\sum _{j=1}^{\infty} (1-x_j T^j) \right ) = (x_1,x_p,x_{p^2},x_{p^3}\dots).$$

LEMMA 09.4   Let us define polynomials $\alpha_j(X,Y)\in \mathbb{Z}[X,Y]$ as follows.

$$(1-x T)(1-y T)=\prod_{j=1}^\infty (1-\alpha_j(x,y) T^j).$$

Then we have the following rule for ``carry operation'':

$$(1-x T^n)\boxplus (1-y T^n) =\sideset{}{^\boxplus}\sum_{j=1}^{\infty} (1-\alpha_j(x,y)T^{j n}).$$

PROPOSITION 09.5   There exist unique binary operators $\boxplus$ and $\boxtimes$ on $\mathcal W^{(p)}(A)$ such that the following diagrams commute.

$$\begin{CD} \mathcal W_1 (A)\times \mathcal W_1 (A) @>\boxplus » ... ...W^{(p)}(A)\times \mathcal W^{(p)}(A) @>\boxplus » \mathcal W^{(p)}(A) \end{CD}$$

$$\begin{CD} \mathcal W_1 (A)\times \mathcal W_1 (A) @>\boxtimes »... ...^{(p)}(A)\times \mathcal W^{(p)}(A) @>\boxtimes » \mathcal W^{(p)}(A) \end{CD}$$

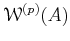
PROOF.. Using the rule as in the previous lemma, we see that addition descends to an addition of $\mathcal W^{(p)}(A)$ . It is easier to see that the multiplication also descends.

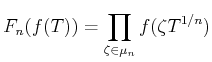
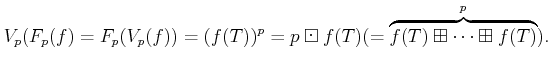
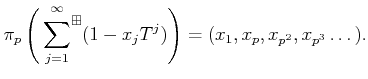
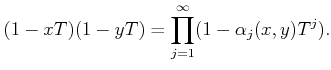
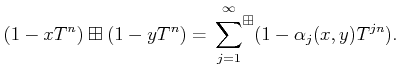
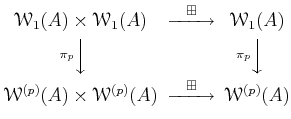
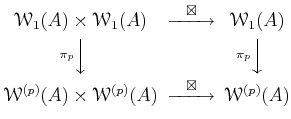
$\qedsymbol$

DEFINITION 09.6   For any commutative ring $A$ , elements of $W^{(p)}(A)$ are called $p$ -adic Witt vectors over $A$ . The ring $(W^{(p)}(A),\boxplus,\boxtimes)$ is called the ring of $p$ -adic Witt vectors over $A$ .